Нестабилна връзка
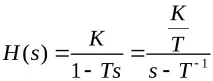
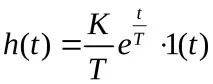
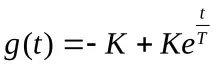
CCH:
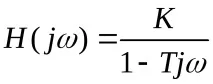
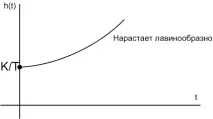
Честотна характеристика:
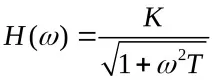
Връзка за 1-ва поръчка>
PFC:
Вибрационна и консервативна връзка.
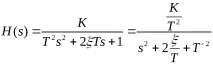
K е статичният коефициент на пренос на сигнала.
T е времевата константа на осцилаторната връзка.
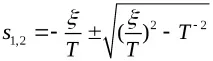
1, тогава връзката ще бъде апериодична връзка от 2-ри ред, в която Т1≠Т2.
Импулсният отговор е линейна комбинация от 2 експоненциално намаляващи функции на времето.
=0, в този случай динамичната връзка се наричаконсервативна.
Импулсният отговор е непрекъсната синусоидална функция на времето.
Честота на естествените вибрации:
(циклична честота)
На консервативно ниво:
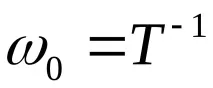
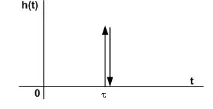
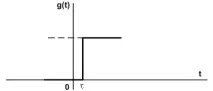
Връзка с чисто забавяне (връзка с идеално забавяне)
K е статичният коефициент на пренос на сигнала.
- време на забавяне на сигнала.
KCHH:
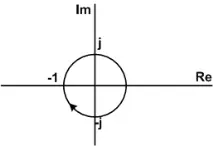
Честотна характеристика:
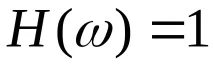
PFC:
По правило елементите и системите с разпределени параметри могат да имат свойствата на забавени връзки. Като електропроводи и комуникационни линии, натоварени с вълнов импеданс.
По правило забавените връзки влошават стабилността на системите с динамична обратна връзка.
Раздел IV Критерии за устойчивост на динамични системи.
Качество на регулиране. Необходимо и достатъчно условие за линейна динамична система.
Всяка динамична система е ефективна само ако е стабилна.
Систематаестабилнаако има ограничен входсигнал, изходният сигнал също е ограничен през цялото време (всички параметри на състоянието на системата са ограничени през цялото време).
Системата за управлениесе наричастабилнаспоред Ляпунов, ако при ненулеви ограничени начални условия свободният компонент на преходния процес в системата е ограничен.
Ако една динамична система е линейно стационарна и ако е устойчива по Ляпунов, то тя естабилна в общия случай.
Линейна стационарна динамична система се описва с линейни диференциални уравнения с постоянни коефициенти.
Систематаестабилнатогава и само ако реалните части на корените на характеристичното уравнение, съответстващо на системата от диференциални уравнения, са отрицателни.
В този случай всички членове на общото решение за свободния компонент на преходния процес клонят към нула, докато времето клони към безкрайност.
Както е известно, на линейно диференциално уравнение от n-ти ред с постоянни коефициенти може да се присвои едно-към-едно съответствие с трансферна функция, чиито полюси са равни на корените на характеристичното уравнение.
В тази връзканеобходимото и достатъчно условие за устойчивостна линейни стационарни динамични системи може да се формулира по следния начин:
Систематаестабилнатогава и само ако реалните части на всички полюси на предавателната функция са отрицателни.
В този случай всички членове на импулсния отговор на системата клонят към нула, докато времето клони към безкрайност.
Полюсите на предавателната функция на стабилна линейна стационарна система се наричат леви полюси, тъй като те са в комплексната равнина вляво отвъображаема ос.
Ако реалната част на полюса е положителна, тогава такъв полюс се наричадесен.
Ако предавателната функция има поне един десен полюс, тогавасистемата е нестабилна, тъй като в този случай поне един от членовете на импулсния отговор клони към безкрайност, както времето клони към безкрайност.
Ако някои полюси на предавателната функция имат нулева реална част, тогавасистемата е на границата на стабилност.
В този случай импулсната характеристика в стационарно състояние е или постоянна функция на времето, или незатихващи периодични трептения.
Ако всички полюси на предавателната функция са реални, тогава преходните процеси в системата протичат без свободни трептения.
Ако най-малко два полюса на предавателната функция са сложни, тогава свободният компонент на преходните процеси има колебателни компоненти.
Критерии за алгебрична стабилност.
Директното прилагане на необходимото и достатъчно условие за стабилност може да бъде придружено от някои трудности, свързани с необходимостта от изчисляване на корените на полиноми от висок ред. Тази процедура е числено нестабилна в много случаи.
Критериите за алгебрична стабилност позволяват да се идентифицира наличието на десни или въображаеми (централни) полюси чрез коефициентите на знаменателя на трансферната функция на затворена система, без да се изчисляват тези полюси.
Тестът на Раут ви позволява да определите аналитично дали всички корени на полинома на знаменателя имат отрицателни реални части. И ако не, колко корена имат положителна реална част.
Този критерий не може да се приложи, когато системата съдържа идеална забавена динамикавръзки.
Тестът на Routh се прилага към полином от формата: