Някои особености на структурния анализ на механизмите

Общи разпоредби

Механизмът се състои от отделни връзки, чието относително движение е ограничено. Подвижна връзка на две връзки, които взаимно ограничават тяхното относително движение, се нарича кинематична двойка. Точките, линията или повърхността, по които връзките влизат в контакт, се наричат ​​​​елемент на кинематична двойка. Ако елементът на една двойка е точка или линия, то той принадлежи към най-високия, а ако повърхността - към най-ниския.

В зависимост от броя на условията за свързване, т.е. от броя на ограниченията, наложени върху относителното движение на връзките, кинематичните двойки се разделят на пет класа. Първият клас включва кинематични двойки, които налагат едно условие на връзка, вторият - две и т.н. Твърдото тяло в пространството има шест степени на свобода. Следователно, броят на условията за свързване, наложени от кинематичната двойка, ще бъде равен на разликата между числото 6 и броя на степените на свобода, които всяка връзка има при относително движение:

Кинематичната верига е система от връзки, свързани помежду си с кинематични двойки. Проста кинематична верига е верига, в която всяко звено е включено в не повече от две кинематични двойки. Сложна кинематична верига е верига, в която има поне една връзка, включена в повече от две кинематични двойки. Простите и сложните кинематични вериги от своя страна се делят на затворени и отворени.

Кинематична верига се нарича механизъм, в който една връзка е превърната в стелаж (неподвижна), а движението на задвижваните връзки се определя изцяло от даденото движение на водещите. Нарича се водеща връзка, за която сумата от елементарните работи на всички приложени към нея външни сили е положителна, а задвижваната връзка е отрицателна или равна на нула.

Броят на степените на свобода на кинематичната верига се определя спрямо връзката, взета като фиксирана. В общия случай формулата за подвижност или структурната формула на кинематичната верига има формата:

къдетоnе броят на движещите се звена на кинематичната верига;

- броят на кинематичните двойки (съответно пети, четвърти и т.н. клас).

За плоски механизми от обща форма структурната формула има формата:

Тази формула се нарича формула на Чебишев. Съгласно формулата, плоските механизми могат да бъдат образувани от връзки, включени само в кинематични двойки от класове IV и V.

Степента на мобилност на механизма се определя от броя на водещите връзки. Водещото звено винаги има само една степен на свобода.

Класификация на плоски механизми с долни двойки

Рационална структурна класификация на плоските механизми е предложена от L. V. Assur. Той се основава на принципа, чиято същност се свежда до факта, че степента на подвижност на оригиналната кинематична верига не се променя от добавянето на друга верига с нулева подвижност към нея (групата на Assur), която отговаря на условието:

Това условие се изпълнява само от следните комбинации от броя на връзките и кинематични двойки:

Таблица 1

n

p5

Първоначалната връзка и стойката, които образуват кинематична двойка от клас V, условно се наричат ​​механизъм от клас I от 1-ви ред (фиг. 1).

Образуването на всеки планарен механизъм може да бъде представено като последователно допълнение към механизма от клас I на групата Assur, който отговаря на условието

Най-простата комбинация от броя на връзките и двойките ще бъдеn= 2,p5 = 3. Като цяло групата Assur с такава комбинация е показана на фиг. 2 и се нарича клас II група от втори ред илидвупосочна група.

Ориз. 1. Схема на механизъм от клас I

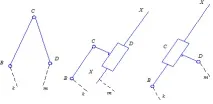
Ориз. 2. Схема на двуводна група и нейните видове

За комбинацияn= 4;p5 = 6 асирийски групи са показани: на фиг. 3 а) група III клас, 3 разряда; б) група IV клас, 2-ри ред.

а) б)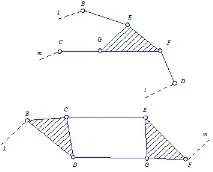

Ориз. 3. Схеми на кинематични групи

Според класификацията на Артоболевски класът на групата на Асур се определя от броя на кинематични двойки, които образуват най-сложния затворен контур, а редът на групата се определя от броя на външните (свободни) кинематични двойки.

Класът и редът на механизма се определя от най-сложната група Assur, включена в механизма.

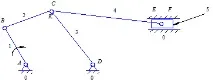
Ориз. 4. Кинематична схема на плосък лостов механизъм

Формулата за структурата на механизма дава визуално представяне на реда на закрепване на кинематични групи (групи на Assur) към водещата връзка и за механизма, показан на фиг. 4 има формата:

Някои характеристики на структурния анализ на механизмите

В случаите, когато механизмът има сложни шарнири (ротационни кинематични двойки), свързващи повече от две връзки, те се състоят от няколко кинематични двойки от клас V, чийто брой се определя като разликаm- 1, къдетоmе броят на връзките. При анализа на механизмите могат да се срещнат пасивни връзки и допълнителни степени на свобода.

Ако степента на подвижност на механизма, определена по формулата на Чебишев, е равна на 0 и механизмът работи нормално, тогава кинематичната верига на механизма има пасивна връзка, която не засяга кинематиката на връзките.

Ако степента на подвижност на механизма с една водеща връзка и нормална работа е повече от една, тогава има допълнителна степен на свобода, свързана, като правило, с наличието на ролки, които могат да бъдатизключено без кинематична повреда на механизма.

Замяна на по-високи двойки с по-ниски

Когато заменяте по-високи двойки с по-ниски, трябва да бъдат изпълнени две условия:

1. Броят на условията на свързване на заместващата кинематична верига трябва да бъде равен на броя на връзките на заменената по-висока двойка (всяка по-висока двойка е еквивалентна на една връзка, включена в двете по-ниски двойки);

2. Относителното движение на връзките, които образуват най-високата двойка, трябва да остане непроменено.

Обобщен метод за получаване на заместващ механизъм: в точката на контакт на кривите се изчертава нормала и върху нея се отбелязват центровете на кривинаO2 иO3. Условната връзка ще бъдеO2O3 с панти в точкатаO2 иO3.

Съдържание на работата

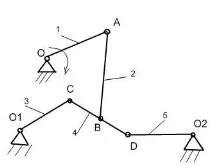
За конкретен многозвезден механизъм: изготвяне на кинематична диаграма, определяне на степента на мобилност, разлагане на групи Assur, определяне на класа и реда, писане на структурната формула, идентифициране на пасивни връзки и допълнителни степени на свобода.

Технология на изпълнение на работата

1. Запознайте се с механизма;

2. Начертайте кинематична диаграма, като означите връзките с арабски цифри, а кинематичните двойки с латински букви;

3. Попълнете таблицата на кинематичните двойки;

4. Определете степента на мобилност на механизма, като използвате формулата на Чебишев

5. Изберете водещата връзка и стойката и разложете останалата кинематична верига на групи Assur. Попълнете таблицата на групите Assur, като определите класа и реда на всяка група и степента на мобилност;

6. Задайте клас и ред на механизма;

7. Напишете формула за структурата на механизма (реда на свързване на кинематични групи);

8. Ако е необходимо, посочете пасивни връзки или допълнителни степени на свобода;

9. Съставяне на отчет.

Ориз. 5. Направо Чебишев

№ п / стр	Обозначаване на двойка на диаграмата	Броят на връзките, образуващи двойка	Име на двойка	Клас по двойки
О	0-1	ротационен	V
А	1-2	ротационен	V
б	2-4	ротационен	V
° С	3-4	ротационен	V
д	4-5	ротационен	V
O1	0-3	ротационен	V
O2	0-5	ротационен	V

Таблица 2

Наличие и характеристики на кинематични двойки

Таблица 3

Наличие и характеристики на кинематични групи (групи на Асур)

№ п / стр	Рисуване и степента на мобилност на групата	Групов клас	Групов ред
	аз	аз
	III	III

Механизъм III клас, III ред

Структура [0-1]-[2,3->на 4 и 5]

Мобилност на механизма

Подвижност (брой степени на свобода) =1; се състои от 2 групи Assur: 1 група = I клас, I ред; 2 група = III клас, III ред;

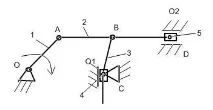
№ п / стр	Обозначаване на двойка на диаграмата	Броят на връзките, образуващи двойка	Име на двойка	Клас по двойки
О	0-1	ротационен	V
А	1-2	ротационен	V
б	2-3	ротационен	V
° С	3-4	ротационен	V
д	2-5	ротационен	V
O1	0-4	Преводачески	V
O2	0-5	Преводачески	V

Наличие и характеристики на кинематични двойки

Таблица 5

Наличие и характеристики на кинематични групи (групи на Асур)

№ п / стр	Рисуване и степента на мобилност на групата	Групов клас	Групов ред
	аз	аз
	III	III
	II	II

Механизъм III клас, III ред

Структура [0-1]-[2,3->на 4 и 5]

Мобилност на механизма

Подвижност (брой степени на свобода) =1; се състои от 3 групи Assur: 1 група = I клас, I ред; 2 група = III клас, III ред; 3 група = II клас, II ред, 2 вида

---