Области на фигури, ограничени от криви линии
Нека сега преминем от многоъгълници към фигури, ограничени от криви линии. И така, разглеждаме някаква затворена крива, която може да се пресича толкова често, колкото желаете; ние му определяме определена посока на заобикаляне и питаме каква зона ограничава.
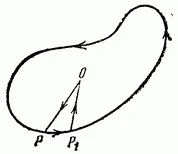
Разбира се, ще намерим тази площ, като апроксимираме кривата (фиг. 14) с многоъгълници с много голям брой много малки страни и като намерим границата на сумата от площите на тези многоъгълници, определени по току-що посочения начин. Ако има два съседни върха на такъв многоъгълник, апроксимиращ нашата крива, тогава неговата площ ще бъде съставена от сумата от елементарни триъгълници, т.е. изключително от членове на формата
В границата тази сума преминава в криволинейния интеграл
взети по нашата крива в посочената посока; това ни дава дефиницията на областта, ограничена от нашата крива.
За да дадем геометрична интерпретация на тази дефиниция, можем да прехвърлим в този нов случай резултата, който посочихме за многоъгълници: всяка част от областта, затворена вътре в кривата, влиза в интеграла толкова пъти със знак плюс и толкова пъти със знак минус, толкова пъти се описва обратно на часовниковата стрелка или съответно по посока на часовниковата стрелка, когато цялата крива се пресича веднъж в дадена посока.
За проста крива като тази, показана на фиг. 14, този интеграл следователно дава точно площта, ограничена от тази крива със знак плюс.
На фиг. 15 външната част се брои веднъж, а вътрешната се брои два пъти със знак плюс; на фиг. 16 лявата страна получава знак минус, а дясната страна знак плюс, така че като цяло се получава отрицателна площ; на фиг. 17 една част изобщо не трябва да се взема предвид, тъй като за нея се оказва веднъжположителен и друг път отрицателен байпас.
Разбира се, по този начин могат да възникнат и криви с площ, равна на нула, ако например кривата на фиг. 16 беше симетрична спрямо точката на пресичане; този случай сам по себе си не е абсурдно, ако имаме предвид, че цялото определяне на района се основава единствено на целесъобразни конвенции.