Определяне на параметрите на парабола - Студопедия

Ако връзката между характеристиките Y и X е нелинейна и се описва от уравнение на парабола от втори ред, тогава

В този случай задачата се свежда до определяне на неизвестните параметриa,b, c.

Прилагайки метода на най-малките квадрати, получаваме уравнението:

За да се намерят стойностите на неизвестните параметриа, b, с, при които функцията би била минимална, е необходимо частните производни по отношение на тези стойности да се приравнят на нула, т.е.:

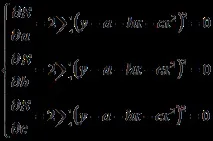
След като направихме трансформациите, получаваме система от нормални уравнения:

След като решихме системата от уравнения, намираме стойностите на неизвестните параметри a, b, c и замествайки ги в, получаваме регресионното уравнение

Оценяването на параметрите на конкретна регресия е само отделна стъпка в дълъг и сложен процес на изграждане на иконометричен модел. Първото оценено уравнение много рядко е задоволително във всички отношения. Обикновено трябва постепенно да се избере формулата на връзката и състава на обяснителните променливи, като се анализира качеството на оценената зависимост на всеки етап. Този анализ на качеството включва статистически и съдържателен компонент. Проверката на статистическото качество на изчисленото уравнение се състои от следните елементи:

- проверка на статистическата значимост на всеки коефициент на регресионното уравнение;

- проверка на цялостното качество на регресионното уравнение;

- проверка на свойствата на данните, чието изпълнение е трябвало да бъде изпълнено при оценяване на уравнението.

Съдържателният компонент на анализа на качеството се разбира като разглеждане на икономическия смисъл на оцененото регресионно уравнение: дали обяснителните фактори, които са важни от гледна точка на теорията, са се оказали значими; положителни или отрицателни коефициенти, показващи посоката на влиянието имфактори; дали оценките на регресионните коефициенти попадат в интервалите, приети от теоретични съображения и т.н.

Помислете за пример за изграждане на прост иконометричен модел:

Постройте иконометричен модел на зависимостта на производителността на труда y от трудовия стаж x на работниците от бригадата по дадени данни, ранжирани по техния трудов стаж.

НомерРабота	Опитработа,години, х	Ежедневнопроизводствоработник,бр, y	X 2	U 2	XY	Ŷ
4ти6ти3ти1ви2ри7ми9ти10ти8ми5ти	12345678910	45677889109	149162536496481100	162536494964648110081	4101828354856729090	4,65,25,86,47,07,68,28,89,410,0
Общо	55	73	385	565	451	73.0

Нека изградим желания модел под формата на уравнение (3.1). Използвайки изчислените стойности

(таблица 1) и съответните формули (3.3) намираме параметрите на уравнението:

а1 = ( 45,1 - 40,15 ) / ( 38,5 - 30,25 ) = 0,6;

Така иконометричният модел на разпределението на продукцията по трудов стажРаботата за този пример може да бъде написана като следното регресионно уравнение:

Правилността на изчислението на параметрите на уравнението може да се провери чрез сравняване на сумите ∑Y = ∑ Ŷ (в този случай е възможно известно несъответствие поради закръгляване на изчисленията).

За практическото използване на регресионните модели от голямо значение е тяхнатаадекватност -съответствие с действителните статистически данни. Може да се провериНадеждността на изградения иконометричен модел

разкъсване с помощта на елементи на дисперсионен анализ

След като изчислим линейния коефициент надвойкакорелация (за линейна регресия) или индекса на корелация(за нелинейна регресия), ние оценяваместегнатостта на връзката между изследваните явления :

Стойността на линейния коефициент (индекс) на двойната корелация е в диапазона от -1 до 1. (от 0 до 1)

Коефициентът (индекс) на определяне е равен на квадрата на коефициента (индекс)на корелацията и показвакакъв процент от вариацията на резултата

на тивния признак y се обяснява с вариацията на фактора x.

Средна грешка на приближение Ā оценява точността на модела и изчислява

се изчислява по формулата:

Ā =Σ Ai/n , Ai = │( уi – уx )/ yi│. 100% (3.8)

Допустимата граница на стойностĀ е не повече от 8 - 10%.

Средният коефициент на еластичностE yxi показва,колко про-

цента средно за населението ще промени резултата y от неговата среда

неговите y стойности и се изчислява по формулата:

E yxi = ai xi / y. ( 3. 9 )

Тъй като корелационният и регресионният анализ, особено в контекста на малкия и средния бизнес, се извършват заограничена по размер популация, тогава параметрите на регресионното уравнение, корелационните коефициенти и детерминациите могат да бъдат изкривени от действието на случайни фактори.

За да проверитестатистическата значимост на коефициентите на регресия и корелация,t - t-тест на Student Оценката се извършва чрез сравняване на оценките на съответните параметри със стойността на тяхната случайна грешка (първият и вторият ред при използване на функцията LINEST). Тази стойност имаt - разпределение на Student с <1 3>n–2 степени на свобода и се наричаt-статистика :

t a1.actual= a1 / Sa1; t a0.actual= a 0 /Sa0; t r.факт. = r/Sr, (3.10)

S a1=S стоп / σx√n - 2, Sa0=S почивка/√p - 2, Sr =√ (1-r 2)/(n-2) ( 3. 11 )

S 2 стоп = Σ( Y – Ŷ) 2 / n

За t-статистиката се тества нулевата хипотеза H0, т.е. твърдението, че стойността на y не зависи от x, тоест a1 = 0. Алтернативната хипотеза Ha е, че a1 ≠ 0, с други думи, че стойността на x влияе върху стойността

г.

Ако t е факт. > t таблица, тогава хипотезата H0 се отхвърля, т.е. коефициент-

Назад към главната страница. или ПОРЪЧАЙТЕ РАБОТА

Деактивирайте adBlock! и обновете страницата (F5)наистина е необходимо

---