Основни логически функции и елементи
2.1 Функция "НЕ", инвертор
Най-простият логически елемент е инверторът, който просто променя стойността на входния сигнал до точно противоположната стойност. Функцията му е написана по следния начин:
,
където лента над входната стойност обозначава промяната на нейната стойност към противоположната. Същото действие може да бъде написано с помощта на таблицата на истината, дадена в таблица 2.1. Тъй като този логически елемент има само един вход, неговата таблица на истината се състои само от два реда.
Таблица 2.1 - Таблица на истинността на логическия инвертор
Като инвертор, в най-простия случай, можете да използвате конвенционален усилвател с транзистор, свързан съгласно верига с общ емитер или източник. Схемата на усилвателя, направена на биполярен n-p-n транзистор и ви позволява да реализирате функцията за логическо обръщане, е показана на фигура 2.1.
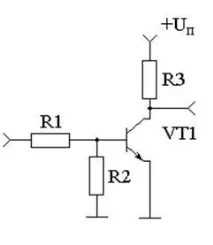
Фигура 2.1 - Схема, която ви позволява да реализирате функцията на логическата инверсия
Инверторните вериги могат да имат различни времена на разпространение на сигнала и могат да работят при различни видове товари. Те могат да бъдат изпълнени на един или няколко транзистора, но независимо от схемата и нейните параметри, те изпълняват една и съща логическа функция.
За да не могат характеристиките на включване на транзистори да затъмняват изпълняваната функция, за цифровите микросхеми са въведени специални условни графични символи. Условното графично представяне на инвертора е показано на фигура 2.2.
Фигура 2.2 - Условно графично представяне на логически инвертор
2.2 Функция "И", логическо умножение
Следващият най-прост логически елемент е схема, която изпълнява операцията на логическо умножение "И":
където символът ^ обозначава функциялогическо умножение (конюнкция). Понякога същата функция е написана в различна форма:
Същото действие може да бъде написано с помощта на таблицата на истината, дадена в таблица 2.2. Формулата по-горе използва два аргумента. Следователно елементът, който изпълнява тази функция, има два входа. Такъв елемент се обозначава с "2I". За елемента "2I" таблицата на истината ще се състои от четири реда. Броят на редовете в таблицата на истината може да се определи по формулата, където N е броят на редовете в таблицата на истината, а n е броят на входовете на гейта. В нашия случай N = 2 2 = 4.
Таблица 2.2 - Таблицата на истината на веригата, която изпълнява
логическа функция "2I"
| x1 | x2 | Е |
Както може да се види от горната таблица на истината, активен сигнал се появява на изхода на този логически елемент само ако, когато и входът x1, и входът x2 ще имат логически единици. Тоест този логически елемент реално реализира операцията "И".
Условното графично представяне на веригата, която изпълнява логическата функция "2I" на схемите на веригата, е показано на фигура 2.3, а отсега нататък веригите, които изпълняват функцията "И" ще бъдат показани в тази форма. Това изображение не зависи от конкретната електрическа схема на устройството, което изпълнява функцията за логическо умножение.
Фигура 2.3 - Условно-графично представяне на веригата, която изпълнява логическата функция "2I"
Най-лесният начин да разберете как работи такъв елемент е със схема, изградена върху идеализирани електронно управлявани ключове, както е показано на фигура 2.4. В горната верига токът ще тече само когато и двата ключа са затворени, което означава, че ниво на единица на изхода на веригата ще се появи само когато се приложи къмнеговият вход е две логически единици.
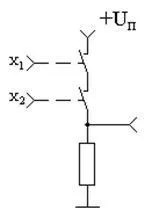
Фигура 2.4 - Еквивалентна схема, която реализира логическата функция "2I"
Функцията за логическо умножение на три променливи се описва по подобен начин:
Неговата таблица на истината вече ще съдържа осем реда (2 3 = 4). Таблицата на истинността на веригата за логическо умножение с три входа "3I" е показана в таблица 2.3, а условното графично представяне на този логически елемент е на фигура 2.5. В този случай в схемата, изградена на принципа на схемата, показана на фигура 2.4, се добавя трети ключ.
Таблица 2.3 - Таблицата на истината на веригата, която изпълнява
логическа функция "3I"
| x1 | x2 | x3 | Е |
Фигура 2.5 - Условно-графично представяне на веригата, която изпълнява логическата функция "3I"
2.3 Функция "ИЛИ", логическо добавяне
Следващият най-прост елемент е схема, която изпълнява операцията "ИЛИ" за логическо умножение:
където символът Ú означава функцията на логическо събиране (дизюнкция). Понякога същата функция е написана в различна форма:
Същото действие може да бъде написано с помощта на таблицата на истината, дадена в таблица 2.4. Горната формула използва два аргумента. Следователно елементът, който изпълнява тази функция, има два входа. Такъв елемент се обозначава с "2OR". За елемента "2OR" таблицата на истината ще се състои от четири реда (2 2 = 4).
Таблица 2.4 - Таблица на истинността на веригата, която изпълнява
логическа функция "2OR"
| x1 | x2 | Е |
Както в случая, разглеждан за веригата за логическо умножение, ще използваме идеализирани електронно управлявани ключове, за да реализираме веригата на логическия елемент 2OR. Този път ще свържем ключоветепаралелен. Еквивалентната схема, която реализира таблицата на истината 2.4, е показана на фигура 2.6. Както може да се види от горната диаграма, нивото на логическа единица ще се появи на нейния изход веднага щом някой от клавишите бъде затворен.
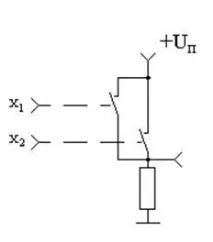
Фигура 2.6 - Еквивалентна схема, която реализира логическата функция "2OR"
Тъй като функцията за логическо сумиране може да бъде реализирана от устройства, сглобени съгласно различни електрически схеми, тази функция се обозначава със собствено конвенционално графично обозначение. На условно-графичното изображение на логическия елемент "ИЛИ" се използва специалният символ "1", както е показано на фигура 2.7.
Фигура 2.7 - Условно-графично представяне на веригата, която изпълнява логическата функция "2OR"
Функцията за логическо събиране на три променливи е описана по подобен начин:
Неговата таблица на истината вече ще съдържа осем реда (2 3 =4). Таблицата на истинността на веригата за логическо умножение с три входа "3OR" е показана в таблица 1.5, а условното графично изображение на фигура 2.8. В схема, изградена като схемата, показана на фигура 2.6, трябва да се добави трети ключ.
Фигура 2.8 - Условно-графично представяне на веригата, която изпълнява логическата функция "3OR"
Таблица 1.5 - Таблицата на истината на веригата, която изпълнява
логическа функция "3OR"
| x1 | x2 | x3 | Е |
Сега, след като разгледахме принципите на конструиране на логически елементи, можем да се спрем подробно на характеристиките на внедряването на логически елементи в различни схемни решения.
| следваща лекция ==> | ||
| Описание на логическата функция на цифровите схеми | Диодно-транзисторна логика (DTL) |
Не намерихте това, което търсихте? Google да ви помогне!