Основни понятия за числено решаване на уравнения

Когато ще използваме приближени методи за числено решаване на уравнения, няма да правим разлика между алгебрични (рационални, ирационални, линейни или нелинейни) и трансцендентни функции.

Така че ще приемем, че уравнението

където функцията f(x) е непрекъсната на сегмента [a; b] и диференцируеми на интервала (a; b).

Необходимо е да се реши уравнение (1), т.е. намерете множеството от всички негови реални корени с дадена точност

> 0.

Универсалните изчислителни алгоритми се основават на започване от някакво първоначално приближениеx0на един от корените, което след това се подобрява (усъвършенства) до необходимата точност.

Както е известно, приблизителното намиране на корените на нелинейното уравнениеf(x)=0обикновено се състои от два етапа:

а)разделяне на корените на уравнението- намиране на достатъчно малки сегменти, принадлежащи към областта на дефиниране на f(x), всеки от които съдържа един и само един корен на уравнението (1).

б)уточняване на приближени корени– изчисляване на корени с предварително зададена точност, ако някои от първоначалните му приближения са известни в интервал, който не съдържа други корени.

Съгласно теоремата на Болцано-Коши [17], ако непрекъсната функция f(x) поеме краищата на сегмента [a; b] стойности с различни знаци, т.е. f(a) f(b) 0 е коренът x* на уравнението F(x) = 0, където F(x) е непрекъсната функция в интервала [a, b]. Приема се, че функцията удовлетворява условието F(a)*F(b)

използване на пространство от имена std;

двойно f(двойно x);

двойна нула (двойно, двойно, двойно);

а=1,2; b=1,5; setlocale(NULL, ".1251");

ако (f(a)*f(c) 0, където F(x) е непрекъсната функция върху [a, b]. Предполага се, че F(a)*F(b) 1, тогава итеративният процес се отклонява.

За конкретен резултатстойността на M (която определя скоростта на конвергенция: колкото по-малко е M, толкова по-бързо е конвергенцията), най-лесният начин е да използвате формулата:

където максимумът е взет за изолационния сегмент на корена [a; b].

Оценявайки φ'(x) за горните четири еквивалентни уравнения, съответстващи на уравнението x³–9x+3=0 (като се има предвид, че коренът на уравнението лежи в интервала [0, 1]), заключаваме, че само второто и четвъртото уравнения са подходящи за прилагане на итерационния метод към тях; за останалите уравнения, итеративният процес ще бъде различен.

Процесът на итерация обикновено продължава до условието

,

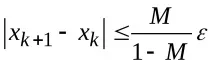
където

е необходимата точност на изчислението, aM= max φ'(x) , x[a; b]

Ако изчисляването на производната φ'(x) и нейната оценка са трудни, тогава е възможно да се ограничи броят на повторенията до определен брой, например n ≤ 500.

Тук представяме две решения на проблема. Първият (опростен) вариант не използва оценката на производната φ'(x). В контролния пример (вижте текста на функцията fi(x)) един от корените на уравнението x - e x + 2 = 0 върху сегмента [-2, 0], а именно x1*  -1.841402, т.е. този корен на сегмента [a, b], където (x) = e x

<inta,b; // наглост, разбира се, но прототипът ще отговаря на типовете

---