Остатъчен член на формулата на Лагранж

Нека оценим разликата

, където t е всяка фиксирана стойност в интервала

, различна от интерполационните възли (таблица).Да приемем, че функцията

в този интервал има производни от всички порядъци до (n + 1) включително.

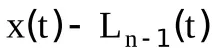
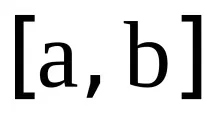
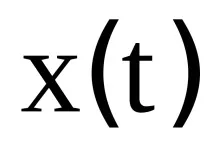
Нека въведем в разглеждането функция - полином от степен n.

Нека изградим спомагателна функция,

където C е const.

също има производни от всички разряди до (n+1)-ти включително.

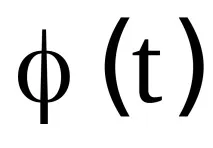
Избираме стойността на константата С така, че за всеки аргумент да се изпълнява

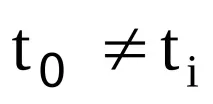
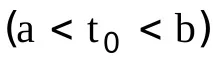
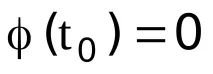
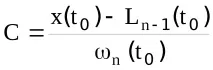
Тъй като

не съответства на нито един възел, тогава

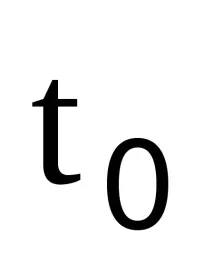
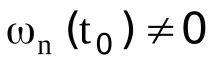
Спомнете си теоремата на Рол.

Ако функцията

е дефинирана, непрекъсната и диференцируема на интервала

и в краищата на този интервал функцията приема равни стойности

, тогава в интервала

има такава точка с (a

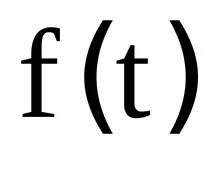
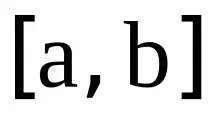
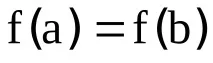
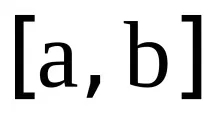
разлики от 1-ви ред

Разлики от 2-ри ред

Разлики от 3-ти ред

Разлики от 4-ти ред

Ако има n стойности на възлите на таблицата, тогава е възможно да се конструира n-1 разлика от 1-ви ред, n-2 разлики от 2-ри ред и само една разлика от n-1 ред.

Функционалните стойности във възлите на таблицата понякога се наричат разделени разлики от 0-ти ред.

ПримерНека изградим таблица с разделени разлики за функцията

за стойностите на аргумента

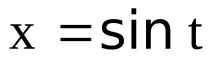
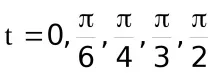
разлики от 1-ви ред

Разлики от 2-ри ред

Разлики от 3-ти ред

Разлики от 4-ти ред

Използвайки дадената таблица

, сега получаваме израз за интерполационния полином на Нютон от n-та степен.

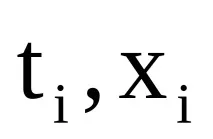
Условието за точкова интерполация изисква желаният полином да премине през всички възли на табличната функция

, [10]

и тъй като са дадени n точки на таблицата, имаме n основни уравнения:

Ако стойностите на функцията

и желанитена полинома

във възлите е еднакъв, тогава техните разделени разлики също трябва да са еднакви:

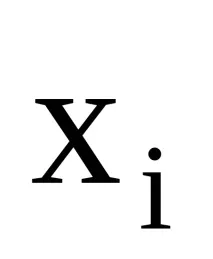
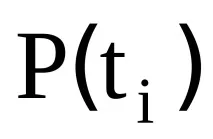
Приравнявайки тези 1-ви разделени разлики, получаваме още n-1 уравнения:

Спомнете си от алгебрата, за да може дробта да бъде намалена до

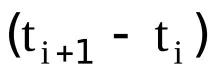
Разделената разлика от 1-ви ред е полином от порядък n-1. По подобен начин може да се покаже, че разделената разлика от i-ти ред е полином от n-i-ти ред. Разделената разлика от n-ти порядък е полином от 0-та степен, тоест постоянно число. Разделените разлики от порядък по-голям от n са 0.

Това свойство на полинома е изключително важно при интерполацията. Табличната функция рядко е полином, но ако е, тогава след съставянето на таблица на разликите се оказва, че разликите от някакъв ред са постоянни числа. Но обикновено табличната функция не е полином и строго постоянните разлики няма да работят. Въпреки това, в повечето задачи табличните функции са такива, че могат да бъдат апроксимирани с полином от известна степен. В тези задачи разликите от някакъв ред ще бъдат почти постоянни, а следващите разлики ще бъдат много малки. Тогава може уверено да се приложи точкова интерполация и да се конструира полином, чиято степен е равна на порядъка на почти постоянните разлики.

Следователно изграждането на таблица на разликите е единственият начин да се намери желаната степен на интерполационния полином, тоест броят възли, необходими за задоволително приближение.

Да предположим, че броят на възлите в таблицата е 3, ние се ограничаваме до специален случай, когато степента на интерполационния полином е n-1=2.

дадено a 2 -b 2 =(a-b)(a+b)