Отговори Урок 10
1. Довършете изреченията
За измерване на разстояния в Слънчевата система се използва астрономическа единица (AU), която е равна на средното разстояние от Земята до Слънцето.
1 a.u. = 149 600 000 км
Разстоянието до обекта според времето на преминаване на радарния сигнал може да се определи по формулата
2. Дефинирайте понятията "паралакс" и "основа"; на фигура 10.1 показват тези количества
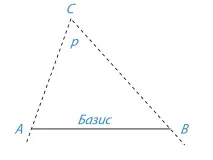
Паралаксът е ъгълът p, под който отсечката AB, наречена основа, ще бъде видима от недостъпно място (точка C).
Основата е внимателно измереното разстояние от точка А (наблюдателя) до всяка точка Б, достигната за наблюдение.
3. Как да използваме концепциите за паралакс и основа за определяне на разстоянието до отдалечен недостъпен обект C (фиг. 10.1)?
Като се има предвид големината на основата и прилежащите ъгли на триъгълник ABC, намерете разстоянието AC. За измервания на Земята този метод се нарича триангулация.
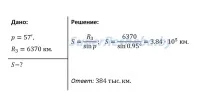
4. Ъгълът, под който светилото S вижда радиуса на Земята, перпендикулярен на зрителната линия, се нарича хоризонтален паралакс p (фиг. 10.2). Определете разстоянията: а) до Луната, ако нейният хоризонтален паралакс е p = 57′; б) към Слънцето, чийто хоризонтален паралакс е p = 8,8″

5. Попълнете фигура 10.3 с необходимите конструкции и извлечете формула, която ви позволява да определите радиуса на небесното тяло (в радиуси на Земята), ако са известни ъгловият радиус на осветителното тяло p и неговият хоризонтален паралакс p
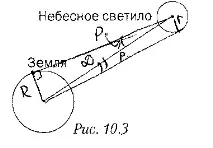
r = D sin(ρ); R = D sin(ρ)/sin(p) R; r = ρ/p R.
6. Решете следните задачи (при пресмятаневземете предвид, че c = 3 105 km/s, R3 = 6370 km)
1. Радарът регистрира отразения сигнал от астероид, летящ близо до Земята след t - 0,667 s. Колко далеч от Земята е бил астероидът по това време?

2. Определете разстоянието от Земята до Марс по време на голямото противопоставяне, когато неговият хоризонтален паралакс е p = 23.2″.

3. При наблюдение на преминаването на Меркурий през слънчевия диск беше установено, че неговият ъглов радиус p = 5,5″, а хоризонталният паралакс p = 14,4″. Определете линейния радиус на Меркурий.

1. Сигналът, изпратен от радара към Венера, се върна след t - 4 min 36 s. Колко далеч беше Венера по това време в долния си съвпад?
Отговор: 41 милиона км.
2. На какво разстояние астероидът Икар се е приближил до Земята, ако неговият хоризонтален паралакс по това време е p = 18.0″?
Отговор: 1,22 милиона км.
3. С помощта на наблюдения е установено, че ъгловият радиус на Марс е p = 9.0″, а хоризонталният паралакс е p = 16.9″. Определете линейния радиус на Марс.