Параметрични кубични криви
За да визуализирате извити линии с помощта на компютър, трябва да знаете тяхното математическо описание.
Има два основни начина за представяне на криви.
Първият начин е да се дефинира крива с помощта на функции на променливиx,y,z:
Този начин на представяне включва много ограничения, особено ако няколко стойностиzсъответстват на някоиxиyкоординати, т.е. ако кривата образува примка. Освен това в някои точки на кривата стойността на тангенса на ъгъла на наклона може да бъде равна на безкрайност.
Тези проблеми са отстранени в случай напараметриченметод за представяне на криви, когато координатитеx,yиzса описани като функции на някакъв параметърt:
С това представяне лесно се описват затворени и многозначни функции и вместо тангенси на наклона се използват тангенти, които никога не са безкрайни.
Математическите сплайнове са функции, използвани за напасване на криви. Тяхното важно свойство е простотата на изчисленията. На практика често се използват сплайнове под формата на полиноми от трета степен. С тяхна помощ е доста удобно да се изчертават криви, които интуитивно съответстват на човешката субективна концепция за гладкост. Терминът "сплайн" идва от английското spline - което означава гъвкава стоманена лента, която се използва от чертожниците за изчертаване на плавни криви, например за изграждане на контурите на кораби или самолети.
Като функции на параметъраtнай-често се използват полиноми от трета степен (кубични):
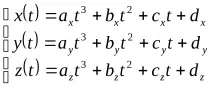
Диапазонът на параметъраtможе да бъде всякакъв, но най-често е ограничен до 0t1. Всички последващи констатации ще бъдат взети предвид за товадиапазон.
Формулите заx(t),y(t) иz(t) са подобни една на друга, така че само уравненията заxкоординатата ще бъдат разгледани по-долу.
Координатите на точките от кривата се описват от вектора [x(t)y(t)z(t)], а трите производни определят координатите на съответния допирателен вектор в точката. Например за координатаx:
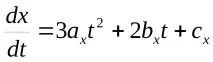
Кривата линия се описва като последователност от отделни сегменти от параметрични кубични криви. В точките на свързване на сегментите трябва да се спазва непрекъснатостта на самата крива (без прекъсвания) и непрекъснатостта на допирателните вектори (без промяна на наклона). Полиноми с по-ниска степен от третата не могат да гарантират, че тези условия са изпълнени. При използване на полиноми от по-високи степени сложността на изчисленията се увеличава и възникват нежелани колебания на кривите.
Има няколко начина за описване на параметрични кубични криви. Нека разгледаме основните от тях: форми на Ермит, Безие и B-сплайнове. Всяка от тези форми има своите предимства и недостатъци.
В рамките наHermite form, кривата се определя чрез координатите на крайната и началната точки (P1 иP4) и стойностите на допирателните в тези точки (R1 иR4). На точките се присвояват индекси 1 и 4 вместо 1 и 2 за съвместимост с изразите, използвани в криви на Безие и B-сплайн. В същото време се приема, че за началната точкаt=0, а за крайната точкаt=1.
Нека пренапишем формулите за функциятаx(t) и тангенсаx(t) в матрична форма:
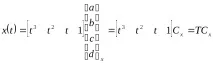
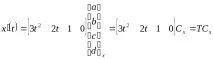
,
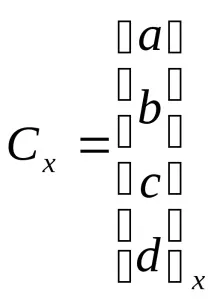
Задачата за конструиране на крива се свежда до намиране на стойностите на елементите на матрицатаCx,т.е. коефициенти ax, bx, cx,dx, отговарящи на условията:
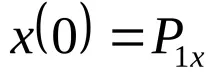
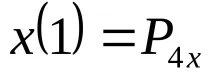
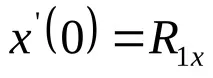
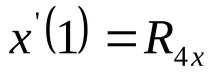
Замествайки тези стойности в (4.5) и (4.6), получаваме:
,
,
,
. (4,8)
Комбинирайки получените изрази в едно матрично уравнение, получаваме:

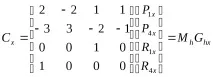
къдетоMhе ермитова матрица,Ghxе ермитов геометричен вектор.
Замествайки резултата в (4.5) получаваме крайното уравнение за координататах:
.(4.11)
Лесно е да промените формата на кривата на Ермит, като се има предвид, че посоката на допирателния вектор определя началната посока, а модулът на допирателния вектор определя степента, до която кривата е удължена в посоката на този вектор, както е показано на фиг. 29.
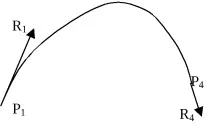
Ориз. 29. Параметричен сплайн във формата на Hermite. Удължаването на кривата надясно се осигурява от факта, чеR1>gt;R4
За да се осигурят условия за непрекъснатост при свързване на сегменти на крива, е необходимо крайната точка на първия сегмент да съвпада с началната точка на втория сегмент, а допирателните вектори към сегментите в тези точки да имат една и съща посока, дължината на векторите може да бъде различна:
Недостатъкът на формата на Hermite е необходимостта от изрично задаване на стойностите на допирателните вектори в крайните точки на кривата, което не винаги е удобно при прилагане на интерактивни режими на приближение, освен това самата концепция за вектор е непозната за някои потребители. Формата на Hermite е полезна за апроксимиране на вече съществуващи криви, когато дължината или посоката на допирателните вектори е приблизително известна.
Безиеизползва четири контролни точки, за да дефинира кубична крива:P1,P2,P3 иP4. Тази форма на определяне на кубична крива е много близка до формата на Ермит, но допирателнитевекторите в крайните точкиR1 иR4 се определят от сегментиP1P2 иP3P4.
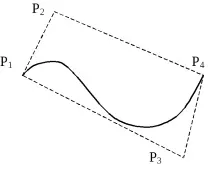
Ориз. 30. Параметричен сплайн във форма на Безие.
ТочкитеP2 иP3 и съответстващите им радиус вектори (както е показано на фиг. 42) се въвеждат по такъв начин, че да са изпълнени следните условия:
Преходът от геометричен вектор на БезиеGbкъм геометричен вектор на ЕрмитGhсе определя като:

къдетоMhbе матрицата на прехода от геометричния вектор на Безие към геометричния вектор на Ермит.
Изразът за функциятаx(t) изглежда така:
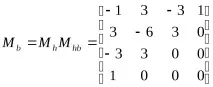
Формата на Безие е най-удобна при апроксимиране на криви, определени от набор от точки. В компютърната графика формата на Безие е по-често използвана от формата на Ермит.
Четирите контролни точки във форма на Безие определят изпъкнала четворка, която съдържа самата крива. Изпъкналият многоъгълник е полезен за много операции, като изрязване на крива към видимия обем. При извършване на тази операция, вместо незабавна проверка на изрязването на кривата, първо се проверява нейната изпъкнала обвивка и само ако изпъкналата обвивка пресича видимия обем, става необходимо да се провери самата крива.
За да се осигурят условия за непрекъснатост при свързване на кривите, е необходимо крайната точка на първия сегмент да съвпада с началната точка на втория сегмент, а точкитеP3 I иP2 II да лежат на една и съща права линия, минаваща през точката на свързване на сегментите:
Формата наB-splineе по-гладка от другите форми на представяне, защото неговият допирателен вектор и кривина имат непрекъснатост на изменението, т.е. първата и втората производни на кривата са непрекъснати в крайните точки, приза разлика от формите на Ермит и Безие, в които само първите производни са непрекъснати в крайните точки.
B-сплайнът се описва със следната формула:
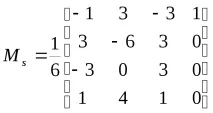
Когато се апроксимират контролни точкиP1,P2, …,Pnчрез последователност от B-сплайнове между всяка двойка съседни точкиPiиPi+1, се използват последователно геометрични матрици:
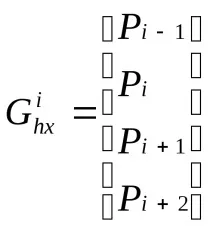
По принцип контролните точки на B-сплайн не лежат на кривата, но при определени условия B-сплайн може да премине презвсякаконтролна точка. B-сплайнът, описан с горната формула, ще премине през контролната точкаPiако точкитеPi,Pi+1 иPi+2 са еднакви. Обикновено формата на B-сплайнове се използва за приближаване на дълги сегменти от криви, дадени от значителен (повече от пет) брой контролни точки.
Най-широко използвани в компютърната графика са така наречените неравномерни рационални B-сплайнове (NURBS-Non-UniformRationalB-Splines) NURBS се използват широко в системите за геометрично моделиране и триизмерната графика.