Поточни шифри

Поток или поточен шифър е шифър, при който резултатът от криптирането на следващата част от данните зависи от самата тази част и от всички предишни данни на криптирания масив, във важен конкретен случай зависи от самата част от данните и от нейната позиция в масива и не зависи от стойността на предишните и следващите части от данни. Понякога това условие се допълва с изискването на една стъпка да се криптира елементарна структурна единица от данни - бит, текстов знак или байт.

Шифроването и декриптирането в такива схеми може да бъде прекъснато в произволен момент, веднага щом се окаже, че предаваният поток е прекъснат, а също и възстановено, когато се установи фактът на продължаване на предаването. Такава обработка на информация може да бъде представена като автомат, който във всеки свой цикъл:

генерира, според някакъв закон, един бит от шифриращата последователност;
наслагва този криптиращ бит върху един бит от отворения поток чрез някаква обратима трансформация, получавайки криптиран бит.

Защо е достатъчно да се ограничи последователността на шифъра само до един бит на бит от отворения текст? Факт е, че в аритметиката по модул 2, която включва всякакви трансформации над битове, има само две обратими операции изключително ИЛИ (на английски изключително ИЛИ - XOR,, което също е събиране по модул 2) и отрицание. Една функция се нарича обратима, ако, знаейки резултата и всички операнди с изключение на един, е възможно да се възстанови този неизвестен операнд.

Очевидно само обратими операции могат да се използват в процеса на криптиране на поток, в противен случай от приемащата страна получателят няма да може да възстанови уникално оригиналния текст от полученото съобщение, дори да знае правилния ключ.

Следователно, без значение колко създаваме битове за криптиранеизходен текст, всички те ще трябва да бъдат насложени върху този бит чрез комбинация от XOR и отрицания. Но отрицанията могат да бъдат вмъкнати в операцията XOR-за всяко a и b:

НЕ (а XOR b) = a XOR (НЕ b) = (НЕ a) XOR b

Следователно, колкото и сложен да е съставът на битовете за криптиране и оригиналния бит, той винаги може да бъде разделен, т.е. д. представят във формата:

p XOR F(g1, g2, g3,…), където p е оригиналният бит (от англ. plain - отворен), gi са битовете за криптиране, F е някаква функция, съдържаща XOR и отрицание като операции. Очевидно е по-логично незабавно да се извърши тази трансформация върху междинните битове gi и да се получи само един бит за криптиране g като резултат. В резултат на това цялата формула за криптиране ще приеме универсална форма: c = p XOR g, където c е криптираният бит (от английски ciphered - криптиран).

Всички съвременни поточни шифри работят по тази схема. Битът за криптиране, получен при всяка нова стъпка на автомата, както и цял набор от такива битове, обикновено се обозначава със символа γ (гама), а самите шифри на потока получиха второ име поради това - гама шифри. Класическият хазартен шифър е например шифърът на Верман. Общата схема на криптиране с поточен шифър е показана на фигура 6.2.2.1.

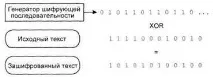
Фигура 6.2.2.1- Шифроване с поточен шифър като цяло

Нека шифроваме думата "котка". Използваме ASCII символни кодове и тяхното двоично представяне:

к - 170 - 10101010;

о - 174 - 10101110;

т - 226 - 11100010.

Тези. последователността за криптиране е: 101010101010111011100010.

За криптиране нека вземем ключа: "abc" - 160,161,162 - 101000001010000110100010. За всеки конкретен алгоритъм ключът се формира по свой начин.

Нека шифроваме с операцията XOR:

Получената последователност се разделя на 8 бита. След това намираме ASCII кодовете на получените числа. Получаваме "UV?".

Ако извършим операцията по дешифриране, използвайки същия ключ, получаваме:

Изходната последователност също е разделена на 8 бита. Получаваме 170, 174, 226 - "котка".

Гама шифрите са много по-бързи от техните най-близки конкуренти, блоковите шифри, ако криптирането на потока е внедрено в хардуера. Основните схеми на гама шифрите са изключително прости и изглеждат като "попитани" за хардуерна реализация - това не е изненадващо, като се има предвид историята и основната цел на тяхното създаване. В случаите, когато по някаква причина тези алгоритми са внедрени в софтуера, тяхната скорост е сравнима с блоковите шифри, а понякога и много по-ниска от тях.

Трите основни компонента, върху които се изчислява функцията за генериране на гама са:

номер на текущата стъпка на криптиране;
битовете от оригинала и/или шифрования текст, съседни на текущата позиция.

Ключът е необходима част от шифъра на играта. Ако ключът и схемата за генериране на гама не са секретни, тогава шифърът на потока се превръща в конвенционален конвертор на енкодер - скрамблер (от английското scramble - смесване, победа). Скрамблерите се използват широко в комуникационните системи за подобряване на статистическите характеристики на предавания сигнал. Честотата на поява на единици и нули в потока, обработен от скрамблера, е близка до (0,5), което дава печалба в качеството на предаване на сигнала. Освен това в много системи за синхронизация са необходими чести промени на нули и единици - в момента, в който стойността (ръбът) на сигнала се промени от "0" на "1" или от "1" на "0", приемащата страна коригира своите тактови генератори. Често по отношение на поточните шифри, по аналогия стакива енкодери използват термина "скрамблер".

Зависимостта на бита за криптиране от номера на текущата позиция, ако има такава, най-често се задава имплицитно. Няма проста формула за определяне на следващия бит от гамата по номера на позицията и ключа. Просто при всеки цикъл на криптиране се извършват някои подобни трансформации върху ключовия материал и вътрешните променливи на шифъра на потока и поради това всеки бит за криптиране всъщност зависи от неговата позиция (номер) в общия гама поток.

Когато се включат в такъв цикъл от трансформации битове от оригинала или шифрован текст, потоковият шифър придобива напълно нови свойства. Обикновено този тип обратна връзка обхваща битове, които не са много далеч от текущата позиция. Това се дължи на факта, че увеличаването на такова разстояние, въпреки че подобрява криптографската сила на шифъра срещу определен тип атака, изисква внедряването на допълнителни клетки с памет, което може да стане обременяващо за хардуерното внедряване.

Матрицата на зависимостта на основните свойства на поточните шифри от идеологията на тяхното изграждане е дадена в таблица 6.2.2.1. Веднага трябва да се отбележи, че описаните свойства зависят от много фактори, включително много силно от специфичната структура на поточния шифър, така че не могат да се приемат за абсолютна истина.

Таблица 6.2.2.1 - Свойства на разновидности на поточен шифър

Гамата зависи от битовете на оригинала или шифрования текст	Гамата НЕ зависи от битовете на оригинала или шифрования текст
Гама зависи от броя на текущия цикъл на криптиране	(-) декодерът губи синхронизация при грешки "вмъкване/липсване на бит" в комуникационния канал (-) декодерът разпространява грешки "битова повреда" в комуникационния канал (+) веригата е устойчива на известна атакапрограмен код	(-) декодерът губи синхронизация при грешка „вмъкване/липсване на бит“ в комуникационния канал (+) декодерът не разпространява грешки „битова повреда“ в комуникационния канал (+) схемата е устойчива на позната атака с обикновен текст
Гама НЕ зависи от номера на текущия цикъл на криптиране	(+) декодерът не губи синхронизация в случай на грешка "вмъкване/липсване на бит" в комуникационния канал (-) декодерът разпространява грешки от класа "битово изкривяване" в комуникационния канал (-) схемата не е устойчива на атака с познат изходен текст

В съвременната практика най-широко се използват шифри с гама, която зависи само от ключа и номера на цикъла на криптиране.

Най-простите схеми, използвани като основа при изграждането на други, по-сигурни, поточни шифри, са линейните регистри за изместване - LRS (на английски linear feedback shift registers - LFSR). Тяхната структура е изключително проста: устройството се състои от няколко (от 20 до 100) клетки с памет, всяка от които може да съхранява един бит информация. Наборът от битове в момента в LRS се нарича неговото състояние. За да генерира следващия бит от последователността за криптиране, т.е. гама, LRS изпълнява един цикъл от трансформации, наречен цикъл, съгласно следния алгоритъм.

Първият (например най-десният) бит от последователността влиза в изхода на LRS - това е следващият бит от гамата.
Съдържанието на всички междинни клетки на паметта се измества с една позиция надясно.
В празна клетка от паметта, възникнала в резултат на изместване на левия край на LRS, се поставя бит, който се изчислява като операция XOR върху стойности от LRS клетки с определено число.

Естествено посоката на смяната не играе никаква роля и можеби било да се формулира целият даден алгоритъм чрез премествания "от дясно на ляво".

Схематично линеен регистър за изместване изглежда както е показано на фигура 6.2.2.2.

Фигура 6.2.2.2 - Общ изглед на линеен преместващ регистър

Броят на битовете, обхванати в LPC чрез обратна връзка, се нарича неговата битова дълбочина. Когато се използва като най-прост шифър, преди началото на процеса, ключът се поставя в клетките на паметта на LRS бит по бит. В резултат на това гама битът, генериран при всеки цикъл, зависи от ключа и от номера на този цикъл в цялостната процедура на криптиране.

При достатъчно продължителна работа на скрамблера неизбежно възниква неговото зацикляне - броят на възможните опции за състоянията на LRS е краен и следователно след определен брой цикли в неговите клетки ще се създаде комбинация от битове, която вече се е появила в него веднъж. От този момент нататък последователността на кодиране ще започне циклично да се повтаря с фиксиран период. Ако представим набора от състояния на LPC и преходите между тях под формата на графика, тогава в зависимост от броя на клетките, които генерират обратна връзка, могат да се получат напълно различни топологии. Някои от тях са показани на фигура 6.2.2.3.

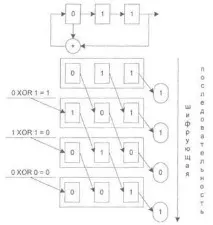
Фигура 6.2.2.3 - Пример за работа на линеен преместващ регистър

Цикълът "000" е типичен за всички графики поради структурата на LPC. На фигура 6.2.2.4 (а) в допълнение към "нулевия" цикъл се виждат още два цикъла - от 3 състояния и от 4 състояния. На фигура 6.2.2.4 (b) веригата се сближава към цикъл от 3 състояния и никога не излиза оттам. И накрая, на фигура 6.2.2.4 (c), всички възможни състояния, с изключение на нулата, са комбинирани в един затворен цикъл. Очевидно е, че в този случай, когато всички 2 N -1 състояния на системата (където N е капацитетът на LRS), с изключение на нулевия, образуват един цикъл, периодът на гама повторение е максимален и корелациятамежду дължината на цикъла и първоначалното състояние на регистъра (т.е. ключа), което би довело до по-слаби ключове.

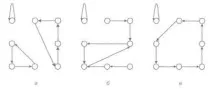
Фигура 6.2.2.4 - Графики на линейни регистри за изместване

От многото PND генератори с даден капацитет, в моменти, когато са били реализирани на електрическа или минимална електронна основа, са избрани схеми с минимален брой кранове за обратна връзка. Обикновено HDPE генератор с желана битова дълбочина може да бъде постигнат с 2, 3 или 4 крана. Въпреки това, много големи разстояния между крановете за обратна връзка, които неизбежно се появяват, когато комбинацията от малък брой кранове и голяма дълбочина на битовете на LRS, също могат да повлияят неблагоприятно на устойчивостта на криптиращата последователност към криптоанализа.