Повърхностен определител - Studiopedia
Кинематичният начин на формиране на повърхност може да бъде представен като набор от позиции на движеща се линия или повърхност.
Този метод дава възможност да се формулираконцепцията за повърхностна детерминанта. Това понятие обикновено означаванеобходим и достатъчен набор от геометрични форми и кинематични връзки между тях, които уникално определят повърхността.
Повърхностният детерминант се състои от две части:
Геометрична част - набор от геометрични форми, които могат да се използват за формиране на повърхност.
Алгоритмична част - алгоритъм за формиране на повърхнина чрез фигури, включени в геометричната част на детерминантата.
За да се намери детерминантата на повърхността, трябва да се изхожда от кинематичния метод на образуване на повърхността.
За да се изгради чертеж на повърхност, е необходимо първо да се идентифицира нейната детерминанта. Детерминантата на повърхността се разкрива чрез анализ на методите за формиране на повърхността или нейните основни свойства. Като цяло една повърхност може да се формира по няколко начина и следователно може да има няколко детерминанти. Обикновено от всички методи за формиране на повърхността се избира най-простият.
Една повърхност се счита за дадена в сложен чертеж, ако по отношение на която и да е точка от пространството, дадена в чертежа, е възможно недвусмислено да се реши дали тя принадлежи към тази повърхност. Построяването на проекции на всякакви точки и линии, принадлежащи на повърхнината, както и втората им проекция, ако е дадена, се извършва въз основа на нейната детерминанта.
Точка принадлежи на повърхност, ако принадлежи на линия, принадлежаща на повърхността.
Обмислете примери за определяне на детерминанта за някои от най-проститеповърхности:
Чрез три точки A, B, C, които не принадлежат на една и съща права линия, може да се начертае една и само една равнина (на фиг. 7.3, а). Точки A, B и C съставляват геометричната част на равнинната детерминанта.
Втората част от детерминантата, т.е. алгоритъмът за построяване на произволни прави и точки в равнината (A, B, C), се изразява с предварително разгледаните условия за принадлежност на права и точка към равнината.
На чертежа (фиг. 7.3, b) равнината е дадена от проекциите на геометричната част на нейната детерминанта: A (A1A2), B (B1B2), C (C1C2).
Цилиндрична повърхност на въртене може да се образува чрез завъртане на правата линия 1 i около оста i (фиг. 7.4, а).
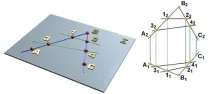
Фиг.7.3. Примери за детерминанта: а - алгоритмична част; b - геометрична част
Геометричната част на детерминантата на повърхността се състои от образуваща 1 и ос i. Алгоритмичната част на детерминантата се състои от въртенето на образуващата на линия 1 около оста i.
Детерминантата на цилиндрична повърхност на въртене има формата Ф(l i, i) [A]. На чертежа (фиг. 7.4, b) ротационният цилиндър е даден от проекциите на геометричната част на неговата детерминанта.
Конична повърхност на въртене може да се образува чрез въртене на права линия l, пресичаща оста на въртене i под определен ъгъл (фиг. 7.5, а). Алгоритмичната част на детерминантата се състои от словесна индикация, че повърхността е образувана чрез въртене на образуващата l около оста i.
Детерминантата на конична повърхност на въртене има вида Ф( l ∩ i)[A].
На чертежа (фиг. 7.5, b) конусът на въртене е даден от проекциите на геометричната част на неговата детерминанта:
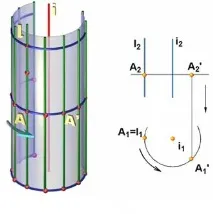
Ориз. 7.4. Детерминанта на цилиндрична повърхнина: а - повърхнината се образува от въртенето на правата l i около оста i; b - цилиндърът на въртене е даден от проекциите на геометричната част на неговиядетерминант
В тези примери детерминантата на повърхността се определя чрез анализ на методите за нейното формиране. Помислете за пример за идентифициране на повърхностна детерминанта чрез анализиране на нейните основни свойства. Вземете например сфераСферата е повърхност, образувана от набор от точки в пространството, разположени на разстояние r от дадена точка О (фиг. 7.6, а)Геометричната част на детерминантата на сферата се състои от точка О (центърът на сферата) и точка М, принадлежаща на нейната повърхност. Алгоритъмът за конструиране на произволна точка от сферата се състои в начертаване на произволна права линия през точката O и полагане върху нея от точката O на сегмента OM' = OM = r. Детерминантата на сфера има вида Ф(О, М) [A]. На фиг. 7.6, b (вдясно) сферата е дадена от проекциите на точките O (O1O2) и M (M1M2), които съставляват геометричната част на нейната детерминанта, и е показана конструкцията на произволна точка M n (M n 1 M n 2) на сферата. Когато четете чертеж, неговата яснота играе важна роля. Дефинирането на повърхност чрез проекции на геометричната част на нейната детерминанта не осигурява яснота на изображенията. Ето защо, за да направят рисунката на повърхността по-ясна и изразителна, те прибягват до конструиране на скици на нейните проекции или проекции на достатъчно плътна рамка на нейните генератори.
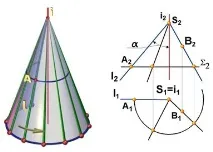
Ориз. 7.5. Изображение на детерминантата на конична повърхност:
а - алгоритмична част; b - геометрична част
Когато една повърхност се проектира върху която и да е проекционна равнина, част от проектиращите лъчи я докосват, образувайки проектираща повърхност. В този случай точките на контакт образуват линия на видимия контур на повърхността спрямо тази равнина на проекции (фиг. 7.7). Контурът на повърхностната проекция е проекцията на съответната видима контурна линия. Линията на видимия контур на повърхността я разделя на две части - видимата, лицеванаблюдател и невидим. Никоя точка от повърхността не може да бъде проектирана извън контура.
На чертежите (фиг. 7.8, a, c) конусът на въртене и сферата са дадени от проекциите на геометричната част на тяхната детерминанта, а на чертежите (фиг. 7.8, b, d) са изградени очертания на техните проекции за същите повърхности. Последните, разбира се, имат повече видимост и изразителност.
Кривите повърхнини се делят на линейни и нелинейни, правилни и неправилни.Повърхност се нарича линейка, ако може да бъде оформена чрез преместване на права линия, в противен случай нелинейка.
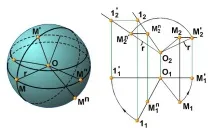
Ориз. 7.6. Изображение на сферична детерминанта: a - алгоритмична част; b - геометрична част
Ако повърхнината може да се определи с някакво уравнение, тя се нарича правилна, в противен случай - неправилна или графична (посочва се само чрез чертеж).
Правилните повърхности в зависимост от вида на уравнението се делят на алгебрични и трансцендентални.
Алгебрично уравнение от n-та степен (в декартови координати) дефинира алгебрична повърхност от n-ти ред (трансценденталните повърхности нямат ред). Алгебрична повърхнина от n-ти ред се пресича от равнина по крива от n-ти ред, а с права - в n точки.
Равнина, която има уравнение от първа степен (пресича се с произволна равнина по права линия и с права линия в една точка), може да се разглежда като повърхност от първи ред. Примери за криви повърхности от втори ред са повърхности, образувани от въртенето на криви от втори ред около една от техните оси.
Повърхнините от втори ред се пресичат с произволна равнина по криви от втори ред, а с права линия - в две точки. Пример за повърхностможе да служи тор от четвърти ред (виж повърхности на въртене).
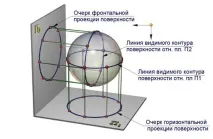
Ориз. 7.7. Образуване на сферични проекции
Детерминантата може да се използва като основа за класификация на повърхности. Същият клас включва повърхности, които имат една и съща определяща структура.
Най-голямото приложение в технологията е получило кинематични извити повърхности с генератори с постоянна форма:
1. Линейни повърхности:
a) с възможност за разгръщане;
b) без възможност за разгръщане;
B) винт.
Не намерихте това, което търсихте? Използвайте търсачката:
Деактивирайте adBlock! и обновете страницата (F5)наистина е необходимо