ПРАКТИКА

Практическа работа №1

Въз основа на дадени диференциални уравнения определя операторни уравнения при нулеви начални условия, трансферни функции, блокови диаграми на връзки, техните характеристични уравнения и корени на характеристични уравнения.

Примерно решение на задача

Дадено е диференциално уравнение, което характеризира динамиката на някакъв технологичен обект,

.

Записваме оригиналното диференциално уравнение в операторна форма:

Това уравнение може да се преобразува чрез изваждане наyиxизвън скоби:

.

Ако обозначим трансферните функции на обекта като

,

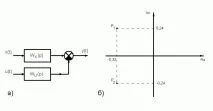
Получените трансферни функции имат едни и същи знаменатели, наречени характеристични изрази:

Ако приравним този израз към нула, тогава се образува характеристичното уравнение2p+ 1 = 0, корените на което

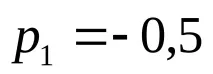
Дадено е диференциално уравнение, което характеризира динамиката на някакъв технологичен обект,

.

Записваме оригиналното диференциално уравнение в операторна форма:

5p2y+ 3py +0,5 y = 2up+4u – 10pf.

Това уравнение може да се преобразува чрез изваждане наyиxизвън скоби:

.

Ако обозначим трансферните функции на обекта като

,

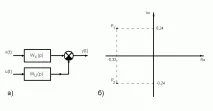
Получените трансферни функции имат едни и същи знаменатели, наречени характеристични изрази:

Ако приравним този израз към нула, тогава се образува характеристичното уравнение5p2+ 3p+ 0,5 = 0, корените на което са

И.

1.а);

б) .

Практическа работа #2

За дадена предавателна функция напишете диференциално уравнение.

Примерно решение на задача

Дадена е предавателна функция на формата

.

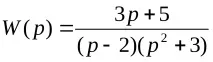
За да се напише диференциалното уравнение, е необходимо да се вземе предвид, че по дефиниция

, откъдето е получено:

,

.

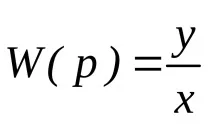
2.

.

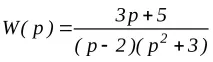
Дадено е едноконтурно ASR, за което се определя предавателната функция на регулатора (P) с настройки и диференциалното уравнение на обекта на управление (OC). Необходимо е да се определи:

- характерен израз на затворена система (CVZS),

- предавателни функции на затворената системаФз(p)– съгласно заданието,

- печалби от АКТБ,

Примерно решение на задача

Даден е PI регулатор с PF във форматаWp= 5 +

и обект на управление, описан от диференциално уравнение

.

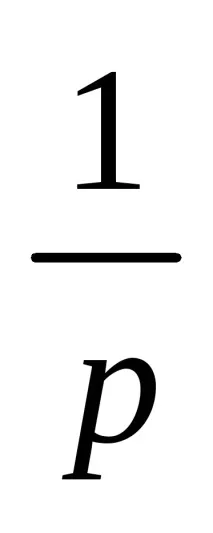
Трансферната функция на обекта се определя:

.

Тогава трансферната функция на отворена система има формата:

.

D (P) = A (P) + B (P)= 4P4 + 8P3 +5P2 + 20P+ P + 4 = 4P4 + 8P3 + 5P2 + 21p+ 4.

Трансферни функции на затворена система:

- по задание

- по погрешка,

- от възмущение.

Трансферните функции се използват за определяне на печалбите чрез заместване наp= 0 в тях:

Стабилността на ACP се определя от критерия на Хурвиц.

(обърнете внимание на сходството на редовете на матрицата: 1 с 3 и 2 с 4). Квалификатори:

,

Δ4= 1* Δ3= 1*-504

0.

Тъй като всички детерминанти са отрицателни, ACP не естабилен. ♦

Р - PI-регулатор с PF от видаWp= 5 +

;

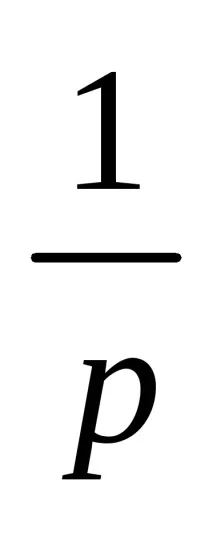
OU диференциално уравнение: .

---