Преглед на надеждността на системата - насоки (N

1. 1000 подобни микросхеми бяха тествани за надеждност. За 3000 часа са се повредили 80 микросхеми, а в интервала от 3000–4000 часа са се повредили още 50 микросхеми. Определете основните показатели за надеждност на този тип елементи в рамките на 4000 часа.
2. 100 артикула от един и същи тип бяха подложени на тест. За 4000 часа 50 продукта са се провалили. В интервала от 4000–4100 часа други 20 продукта се повредиха. Необходимо е да се определи честотата и интензивността на повредите на продукта в интервала от 4000–4100 часа, както и вероятността за безотказна работа и вероятността за повреда на продуктите за първите 4000 часа и за 4100 часа.
3. 45 продукта бяха подложени на тест. За време t = 75 h 44 продукта са се провалили. През последващия интервал от време Dt = 5 h, 1 продукт се провали. Необходимо е да се изчисли вероятността за безотказна работа за времето t и t + Dt, честотата на отказ и честотата на отказ на интервала Dt.
4. Безусловната плътност на разпределение на вероятността за повреда на локалната мрежа се описва с израза f(t) =
= 0,2 10–3(1-exp(-0,0006 t)). Намерете средното време до първата повреда на локалната мрежа.
5. В резултат на анализа на данните за повредите на компютъра беше установено, че честотата на повредите му се описва с израз на формата f(t) =
= 2le–tl (1–e–tl). Необходимо е да се определят основните количествени характеристики на надеждността на компютъра.
6. В резултат на анализа на данните за отказите на компютърната система беше установено, че вероятността за безотказна работа се изразява с формулата P(t) = 3e–tl – 3e–2tl + e–3tl . Намерете количествени характеристики на надеждността на изчислителната система.
7. Степента на отказ на продукта зависи от времето и се изразява чрез функцията l(t) = k(1–e–tk) / (0,5–e–tk). Необходимо е да се определят количествените характеристики на надеждността на продукта.
8. В резултат на наблюдение на 45проби от оборудване, получени данни за времето между отказите на всичките 45 проби, които са обобщени в таблицата. Определете вероятността за безотказна работа, честотата на отказите и честотата на отказите като функция на времето, начертайте тези функции и идентифицирайте закона за разпределение на времето между отказите, както и намерете средното време до първия отказ на този тип оборудване.
9. Времето до отказ на продукта има пресечено нормално разпределение с параметри m = 1000 h и d = 20 ч. Намерете надеждността на продукта при t = 200; 300; 400 часа.
10. Времето на работа на компютъра до отказ се подчинява на закона на Релей с параметър d = 1200 ч. Определете основните характеристики на надеждността на компютъра при t = 10004; 2000 часа.
11. Времето на работа на принтера се подчинява на закона на Вейбул-Гнеденко с параметри k = 1,5, l0 = 0,0001 1/h. Определете основните количествени характеристики на надеждността на принтера.
12. За целия период на наблюдение на РС са регистрирани 13 повреди. Преди началото на наблюдението компютърът е работил 140 часа. До края на наблюдението неговият MTBF беше 1500 часа. Определете средното време между отказите на компютъра.
13. За целия период на наблюдение на три принтера от един и същи тип са регистрирани 8 повреди на първия принтер, 7 повреди на втория принтер и 4 повреди на третия принтер. MTBF на първия принтер е 230 часа, на втория - 380 часа, на третия - 170 часа.Определете MTBF на този тип принтер.
14. Изчислителната система се състои от четири компютъра. Отказът на всеки компютър води до отказ на цялата система. За 870 часа работа са регистрирани 22 отказа на първия компютър, за 660 часа - 12 отказа на втория компютър, а останалите компютри са отказали съответно 5 и 7 пъти за 340 часа работа. Определете времето между отказите на изчислителната система като цяло, ако потокът от откази на всеки компютърописва се с експоненциален закон.
15. Компютърната система има средно време между откази от 600 часа и средно време за възстановяване от 8 часа. Определете коефициента на наличност на изчислителната система.
16. Безусловната плътност на разпределение на вероятността от повреда на компютъра има формата f(t) = С1·l1·exp(–l1t) + С2·l2·exp(–l2t). Определете количествените характеристики на надеждността на компютъра.
17. Системата се състои от три независими елемента, чиито плътности на разпределение на времето за повреда са съответно f1(t) = 1, f2(t) = 2t, f3(t) = 2(1–t) при 0 l2; ако вторият принтер се повреди, степента на отказ на първия също се увеличава до l11>gt; l1. Определете надеждността на тази част от компютъра.
36. Определете условията, при които е препоръчително паралелното (серийно) свързване на три кондензатора
в сравнение с единичен нередундиран кондензатор, ако е известно, че вероятността за безотказна работа на кондензатора P и веригата не е критична за промяна в капацитета.
37. Дадено е: l е степента на отказ на кондензатора; l0, l3 са честотите на повреда на кондензатора, съответно поради отворено или късо съединение; j0 = l0/ (l0 + l3) е вероятността произтичащият отказ да възникне поради счупване. Приема се, че няма последействие от повреди. Определете надеждността на вериги 1 и 2 за свързване на кондензатори.
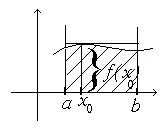
Схема 1 Схема 2
38. Резервираната изчислителна система се състои от един основен и три резервни компютъра. Основният компютър има процент на отказ l1. Всеки от резервните компютри е подложен на поток от повреди с интензитет l2 преди да бъде пуснат в експлоатация. След включване на резервния компютър този интензитет се увеличава до стойността l3. Определете надеждността на изчислителната система.
39. Устройството се състои от два еднакви възела, всеки от коитоможе да се повреди под въздействието на най-простия поток от повреди с интензитет l. Времето за ремонт на повреден възел се разпределя съгласно закона на Ерланг от втори ред f(t) = m2 t exp(-mt). Определете надеждността на устройството.
40. Компютър, който непрекъснато извършва текущи изчисления, се дублира от същия компютър, който е в „горещ режим на готовност“, за да се увеличи надеждността. Степента на отказ на всеки компютър е равна на l с експоненциален закон за надеждност. За включване на резервния компютър се използва превключващо устройство, което е обект на два вида повреди. Отказите от първия тип винаги водят до излизане от нормалното функциониране на цялата изчислителна система с интензивност l1. Вторият тип повреди води до невъзможност за свързване на резервен компютър с интензитет l2. Определете вероятността за безпроблемна работа на изчислителната система.
41. Основният ненадежден елемент на непрекъснато работеща изчислителна система е принтерът. Възстановяването на устройството се състои в проста подмяна на касетата от наличните m резервни. Времето до повреда и времето за смяна на касетата са разпределени експоненциално с параметри съответно λ и μ. Намерете вероятността за безпроблемна работа на системата.
42. Намерете надеждността на компютърна система, състояща се от n компютъра с един ненатоварен резервен компютър, ако възстановяването се извършва след отказ на два компютъра. Общата продължителност на възстановяването на компютъра се подчинява на експоненциален закон с параметър μ. Разгледайте случая със зареден резерв. Степента на отказ на компютъра и резервния компютър е λ.
43. Информационната система позволява непрекъснато наблюдение чрез сигнални светлини без изключване на системата за проверка. Системата за управление може да даде фалшив сигнал с процент на отказ λ0, докато процентът на отказ на самата система– λ1. Намерете коефициента на наличност на системата, ако скоростта на възстановяване на фалшиви и реални повреди е равна съответно на μ1 и μ2. Разгледайте случая на зареден резерв, случая на един и два екипажа за възстановяване, а във втория случай поддръжката е в съответствие с възникването на повреда.
44. Има едноканална стабилизираща система, която позволява компенсиране на отказите на параметричния канал с помощта на устройство за самонастройка. Намерете вероятността за безотказно функциониране на системата, ако потокът от параметрични откази, потокът от внезапни откази на канала и зареждането и потокът от автоматични възстановявания на канали са най-прости с параметри съответно λ1, λ2, λ3 и μ.
45. Изчислителната система се състои от пет едновременно работещи компютъра. Ако някой от компютъра се повреди, възстановяването му започва с постоянен интензитет μ0. Продължителността на безотказната работа на компютъра се подчинява на експоненциалния закон с параметър λ0. Намерете вероятността за безпроблемна работа на системата, ако един от компютрите е резервен.
46. Има изчислителна система, състояща се от 4 блока с проценти на отказ λi, i = 1, 2, 3, 4. Намерете коефициента на наличност, ако по време на възстановяването на един от блоковете останалите са в зареден режим и също могат да се провалят. Броят на персонала е неограничен. Скорост на възстановяване на всеки блок μ.
47. Всеки комплект оборудване има процент на отказ λ, процент на възстановяване μ. Системата се обслужва от един екип, като в началния момент всички комплекти са изправни. За да се осигури непрекъсната работа, резервът трябва да бъде зареден. Колко комплекта оборудване ще са необходими, за да се осигури надеждност, надвишаваща даденото P?
48. Продължителност на безотказната работа на всяко устройство и общовремето за възстановяване на двете устройства се подчинява на експоненциалния закон с параметрите съответно λ и μ. Определете надеждността на цялата система (излишна система с ненатоварен резерв), която се възстановява от повреда на основното и резервното устройство.
49. Определете коефициента на готовност на непрекъснато работеща изчислителна система, ако след всеки втори отказ се извършва основен ремонт с интензивност μ. Честотата на отказ на системата след основен ремонт е λ1, а след престой е λ2. Интензитетът на възстановяване на изчислителната система с обикновен ремонт е μ1.
50. Оборудването на вграденото управление на компютърна система сигнализира за повреда само в σ\% от случаите. Неоткрити повреди се отстраняват след повреда на контролирани елементи или органи за управление и след пълна проверка на системата със специално оборудване, докато компютърната система и управление се възстановяват един по един. Определете коефициента на готовност на изчислителната система по експоненциалните закони на разпределение на времето до повреда и времето за възстановяване на системата и управляващото устройство с параметрите съответно λ1, λ2, μ1 и μ2. Продължителността на фалшива проверка на здрава система се описва с експоненциален закон с параметър μ3.
51. За подобряване на надеждността на изчислителната система се използва резервен компютър, който работи до отказ на системата в "горещ" режим на готовност. Има устройство за управление и превключване, чиято повреда води до една от следните ситуации: извършва се фалшиво превключване (с постоянен интензитет λ); ако в същото време резервният компютър вече се възстановява или проверява, тогава системата се проваля; подава се фалшив сигнал за повреда на резервния компютър с постоянен интензитет λ1; няма да бъде свързанрезервен компютър при реален или фалшив отказ на основния компютър с постоянен интензитет λ2. Намерете надеждността на компютърната система, ако честотата на отказ на компютъра в основния и резервния режим е постоянна и е равна съответно на λ3 и λ4. Скоростта на възстановяване е μ, скоростта на тестване след фалшиво превключване или фалшив сигнал за повреда на компютъра в режим на готовност е μ1.
52. Изследва се надеждността на захранващ блок, състоящ се от понижаващ трансформатор, дросел и два кондензатора с интензитети на отказ λ1, λ2, λ3, λ4 и средно време на смяна съответно μ1, μ2, μ3, μ4. Разрушаването на някой от кондензаторите води до изгаряне на трансформатора. За да се увеличи надеждността на захранването, кондензаторите се резервират чрез свързване на още един кондензатор последователно към всеки от тях, докато поради намаляване на натоварването на напрежението, техните нива на повреда се увеличават съответно до стойностите λ5, λ6. Уредът се обслужва от един ремонтен екип. Кондензаторът може да се повреди само поради повреда. Ремонтът може да започне само след повреда на цялото устройство като цяло и се извършва до пълното възстановяване на устройството.
53. За подобряване на надеждността на измервателната система се използва схема за групиране на еднотипни устройства от три до две с четвърто от същото устройство, разположено в ненатоварен резерв и способно да замени всяко от повредените устройства. λ1 е степента на отказ на едно устройство, когато устройствата на веригата за групиране са в добро състояние, λ2 е степента на отказ на едно устройство, когато веригата за групиране работи с едно повредено устройство. Определяне на показателите за надеждност на измервателната система.