Презентация на тема - Полуправилни многостени - по математика

Изтегляне на презентация (9.85 Mb)
169 изтегляния
4.0 оценка

Анотация към презентацията

Презентация за ученици на тема "Полуправилни многостени" по математика. pptCloud.ru е удобна директория с възможност за безплатно изтегляне на презентация на powerpoint.

Съдържание

Проект на тема: Полуправилни многостени

Изпълнил: Илменская Наталия, 10 клас.

Полуправилен многостен е многостен, в който всички негови многостенни ъгли са равни един на друг (но не непременно правилни), а всичките му лица са правилни многоъгълници (но не всички са равни помежду си).

За първи път полуправилните полиедри са открити от Архимед, древногръцки математик, физик и инженер от Сиракуза, който прави много открития в геометрията и в други области. Ето защо тези полиедри бяха наречени архимедови тела.

Групи от архимедови тела.

Първият от тях се състои от пет полиедра, които се получават от Платоновите тела в резултат на тяхното съкращаване. Включва: Срязан куб. Пресечен октаедър. Пресечен икосаедър. Пресечен тетраедър. Пресечен додекаедър.

1) Срязан куб - съставен от 8 правилни триъгълника и 6 правилни осмоъгълника

2) Пресечен октаедър е многостен, съставен от8 правилни шестоъгълника и 6 квадрата.

3) Пресечен икосаедър многостен, състоящ се от 12 правилни петоъгълника и 20 правилни шестоъгълника.

4) Пресечен тетраедър – състои се от 4 правилни триъгълника и 4 правилни шестоъгълника.

5) Пресечен додекаедър – състои се от 20 правилни триъгълника и 12 десетоъгълника.

Друга група архимедови тела се състои от две тела, наречени квазиправилни полиедри.Тя включва: 1. Кубоктаедър.2. Икозидодекаедър.

1) Кубоктаедър - състои се от 8 правилни триъгълника и 6 правилни квадрата.

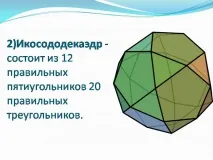
2) Икозидодекаедър - състои се от 12 правилни петоъгълника 20 правилни триъгълника.

Третата група тела включва 2 полиедра, имената на които се различават от имената на предишната група по това, че имат префикса "ромбо", съответно имената им са 1. Rhombicuboctahedron. 2. Ромбикозидодекаедър.

1) Ромбокубооктаедър - състои се от 18 квадрата и 8 правилни триъгълника.

2) Ромбикозидодекаедър - състои се от 12 правилни петоъгълника, 30 квадрата и 20 триъгълника.

Четвъртата група тела се състои от полиедри, наречени "черни" или "черни", такива смешни имена се дават на полиедрите, поради това, че се получават чрез последователно отрязване на всеки от върховете. Това са: 1. Тирнос куб 2. Чистонос додекаедър.

1) Куб с чипсет - състои се от 6 квадрата и 32 правилни триъгълника.

2) Изменен додекаедър - състои се от 12 петоъгълника и 80 правилни триъгълника.

И петата група, най-малката, се състои от един полиедър - 1.Rhombicuboctahedron.

1) Ромбокубооктаедър - състои се от 18 квадрата и 8 правилни триъгълника.

Полуправилни полиедри в живота Несъмнено в нашияВ ежедневието има много полуправилни полиедри и ето няколко примера:

Формата на книгохранилището е ромбокубооктаедър. Библиотеката е най-големият архитектурен ромбокубооктаедър, построен в света днес. Височината му е 73,6 м (23 етажа), а теглото му е 115 000 тона.

Национална библиотека на Беларус.

Музей на архитектурата Тойо на остров Омишима (Япония).

Дизайнът на музея се основава на геометрични форми: октаедър, тетраедър и кубоктаедър.

Сградата на Международния икономически комитет в Киев

Неговият купол на конферентната зала образува с лицата си икозидодекаедър.

Полуправилните полиедри се използват не само в архитектурата, но и в обикновените неща в ежедневието. например:

Фотьойл Hedronics.

Формата на стола е базирана на леко модифициран куб с изпъкнал нос.

По-полуправилни полиедри се срещат в химията, например структурата на различни кристали.