Примери за изграждане на линии на пресичане на една повърхност с друга, Дескриптивна геометрия
Няколко примера са разгледани по-долу, като се използват методите на конструиране, посочени в предходните параграфи, както и специални техники, подходящи за конструиране на точки от желаната линия на определени позиции на повърхности 1).
На фиг. 423 предвид случая, когато проекцията на пресечната линия върху квадрата. π1 съвпада с окръжността - проекцията на цилиндъра с вертикална ос, и върху квадрата. π3 - с полукръг - проекцията на цилиндър с хоризонтална ос. Остава да се намерят точките, чрез които е възможно да се изгради проекцията на желаната линия върху квадрата. π2 (хипербола с връх в точка B").
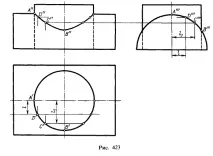
Очевидно проекцията B" се определя директно от проекцията B'", а например проекцията D" се определя като пресечната точка на комуникационните линии, изтеглени от точките D' и D"', координирани от разстоянието l от осите на хоризонталните и профилните проекции.
Също така върху координирани помежду си проекции С' и С"' се определя проекцията С". Както можете да видите, тук не е необходимо да рисувате спомагателни режещи равнини или сфери.
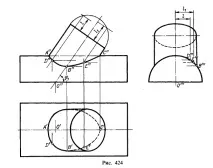
На фиг. 424 за изграждане на проекции B", C", E" са използвани профилни проекции B'", D"', E"', според които са намерени фронталните проекции на образуващата на наклонения цилиндър и проекциите B", D" и E. Имайки проекциите B'", D"', E"', A", B", C", D", E", можете да намерите проекциите A', B', C', D', E'.
В случая, показан на фиг. 425, точките за предните проекции на линиите, по които наклоненият цилиндър пресича повърхността на цилиндъра с вертикална ос, се намират въз основа на позицията на хоризонталните проекции на тези точки. Необходимо е само да се конструират фронтални проекции на съответните генератори на наклонения цилиндър. От точките, отбелязани на фиг. 425, характерните точки са 1 "и 5" - най-близката до оставертикален цилиндър върху видимите и невидимите части на предната проекция на дясната линия, 3 "и 3" - най-много и най-малко отдалечени от квадрата. π1 върху образната на скицата на наклонения цилиндър, 4" и 4", разделящи проекцията на образуващата на скицата на вертикалния цилиндър от проекцията на кривата. Тези точки съответстват на точки със същата стойност на кривата вляво.
На фиг. 426 показва цилиндъра, пресичащ повърхността на конуса. Изходни точки за конструиране на точки 1", 2", . 6" са точки 1', 2', . 6' от хоризонталната проекция на правата върху
1 ) В някои чертежи, за да се спести място, не всички проекции са дадени пълни.
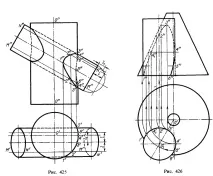
конична повърхност. Например точки 4" и 4"1 се получават върху фронталната проекция на паралела с радиус O'4', точка 3" - върху фронталната проекция на паралела с радиус O'3'.
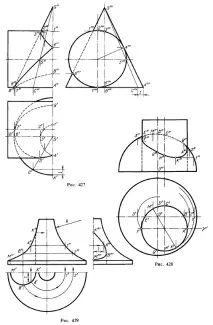
Конструкцията на фронталната проекция на линията на пресичане на цилиндричната повърхност с конус (фиг. 427) е направена според началните точки, взети на профилната проекция на цилиндъра. Точките 1"', 3"', 4"', b'", 8"' позволяват веднага да се намерят характерни точки 1", 3", 4", 6" и 8" за фронталната проекция. Други точки могат да бъдат намерени с помощта на генератори; например, като вземем проекцията S"C" на образуващата, върху която трябва да бъде проекцията 5"', намираме точката C' и проекцията S"'C"' по отсечката l, а след това S"C", остава да получим проекциите 5" и 5'.
На фиг. 428 фронтални проекции на точките от линията, по която цилиндърът пресича повърхността на полусферата, могат да бъдат намерени от хоризонтални проекции върху съответните паралели на сферата. Например, паралел с радиус O'K' се определя от точката K' и проекцията K се намира на неговата фронтална проекция. Същото е показано за точките A и F. Но, разбира се, възможно е, например, за същите точки A и F, отново въз основа на позицията на техните хоризонтални проекции A' и F', да вземем секущия квадрат γ,успореден квадрат. π2 и намерете проекциите A "и F" върху полуокръжността, получена чрез пресичане на pl. γ от повърхността на полусферата. Очевидно в много случаи е препоръчително да се променят методите за конструиране на точки за изчертаване на проекции на пресечни линии, като се избират най-удобните методи, като се стреми към простота и точност на конструкциите.
На фиг. 428 проекции B" и E" се намират на главния меридиан на сферата директно по протежение на точките B' и E'. Също така би било възможно да се намерят проекциите D "и G", ако имаше профилна проекция; сега, без профилна проекция, точки D" и G" могат да бъдат намерени, например, като проекции A" и F".
Отбелязаните на фиг. 428 проекциите A', B', C' и др. определят точките, характерни за челната проекция на кривата и за профилната проекция при нейното конструиране. И така, точки К "и М" - най-ниската и най-високата; в точките B" и E" главният меридиан върху сферата е "прекъснат", а в точките A" и F" пресечната линия е разделена на видима и невидима; точки D", G", C", H" за фронталната проекция не са от особено значение, но ви позволяват да изградите характерни точки върху профилната проекция на кривата.
На фиг. 429 показва въртеливо тяло с цилиндричен отвор в него. Кривата K"A"B"M" е построена от точките K', A', B', M', тоест според известните ни хоризонтални проекции. Например, като вземем точката A', изграждаме проекции на паралел върху повърхността на въртене и върху челната проекция на този паралел намираме проекцията A".
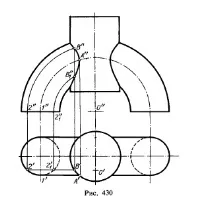
За да се изгради фронтална проекция на линията на контакт между повърхностите на кръговия пръстен и цилиндъра на фиг. 430 използвани хоризонтални проекции на точки (същите като на фиг. 429). Например, знаейки позицията на точка B', можем да начертаем дъги с радиус O'2' и радиус O'2'1 върху повърхността на пръстена и да получим точки B" и B'1 върху тези дъги. Тук използвамесистема от кръгови участъци на повърхността на пръстена.
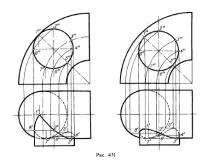
На фиг. 431 също използва факта, че позицията на точките на една от проекциите на желаната права е известна. Това дава възможност да се конструират точки от друга проекция. В случая, показан на фиг. 431 отляво се получава ъглова точка (точка на прекъсване) на хоризонтална проекция.
Построяване на челната проекция на кривата на пресичане на коничната и цилиндричната повърхност на фиг. 432 може да се направи, както е показано например на фиг. 419, т.е. с помощта на сфери, центрирани в точка С. След като построите хиперболата, можете да изградите хоризонтална проекция на кривата, като използвате генераторите на цилиндъра; например, образуващата, върху която е разположена точката E, се определя от отсечката l1.
На фиг. 432 показва друг метод на конструиране, а именно използването напроекция върху допълнителна равнина, в този случай изпъкнала отпред, перпендикулярна на оста на цилиндричната повърхност. Линията на пресичане се проектира върху тази равнина под формата на дъга върху полукръг - проекцията на тази повърхност. Чрез посочване на точки върху дъга могат да се конструират техните хоризонтални и фронтални проекции. Например, като вземем точката E"', определяме сегмента l2 на полукръг с радиус R, който е половин паралел на конуса. Поставяйки сегмента l2 (както е показано на чертежа) на предната проекция, получаваме проекцията E" на линията на комуникация с проекцията E "''.
На фиг. 432 освен това показва развитието на страничната повърхност на пресечения конус, разглеждан в тази задача. Построена е проекция на върха на конуса - точка S "; кръгът на горната основа на конуса се завърта до позиция, успоредна на квадрата π2, и се разделя на няколко части (половината от този кръг е показан на фигурата). Проектирайки точките G2, G3 и т.н. върху линията G "1G" 7, ние чертаем през тези проекции и през S "проекции на образуващите преди среща с проекцията на линията на пресичане на повърхнините; например S"K" се изчертава през G"3.
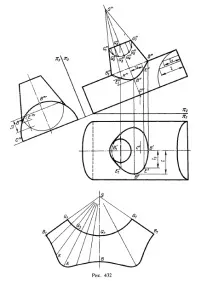
След като изградихме развитие на страничната повърхност на конуса, отделихме дължините на сегментите на генераторите. Например, след като сме намерили дължината на сегмента на генератора G3K чрез въртене, ние го отлагаме съответно в развитието.
На фиг. 433 е нанесена линия на пресичане на четириъгълна призма с цилиндър и развитие на получената част от призмата.
Всяко лице на призмата пресича цилиндричната повърхност в елипса; тези елипси се пресичат една друга в точки, които са точките на пресичане на ръбовете на призмата с цилиндричната повърхност. Фронталните проекции на посочените точки се определят от
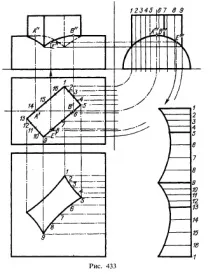
профилните им прогнози. За произволна точка E по нейната профилна проекция E"' определяме проекцията E', а по проекциите E"' и E' намираме E". Точките A" и B" се определят от техните хоризонтални проекции.
За да се изгради размах на призмата, хоризонталната проекция на призмата беше разделена на сегменти и на всяко лице беше взет същия брой деления. Тази разбивка съответства на разбивка на цилиндрична повърхност в зоната на нейното пресичане с призма.
На фиг. 434 е построена линията на пресичане на пирамидата с цилиндъра и развитието на двете повърхнини.
Пресечните линии са елипси, които се пресичат една друга в пресечните точки на ребрата на пирамидата с повърхността на цилиндъра. Точка В” може да се изгради и както е показано на чертежа – без помощта на профилна проекция.
За да се изгради развитието на повърхностите на пирамидата и цилиндъра, кръгът върху хоризонталната проекция на цилиндъра беше разделен на 12 равни части. За да се намерят точки, принадлежащи на елипси, се начертават спомагателни прави линии върху развитието на повърхността на пирамидата презвърха на пирамидата (например права линия SG). Дължината на сегментите на тези линии (например E1 се определя чрез завъртане до паралел на квадрата π2.
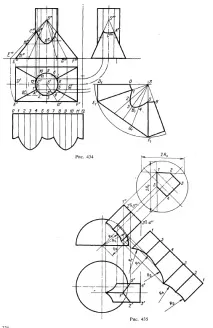
Пример за изграждане на линия на пресичане на призма със сфера и развитие на повърхността на призмата е показан на фиг. 435. Лицата на призмата пресичат повърхността по дъги от окръжности. Проекциите на тези дъги на пл. π1 са части от елипси; проекция на пресечната линия върху квадрата. π2 се състои от части от елипси, дъги от окръжности (тъй като две страни на призмата са успоредни на квадрата π2) и права линия. Намерени са пресечните точки на ръбовете на призмата със сферата. След това трябва да се отбележат точките, които едновременно принадлежат на линията на пресичане на призмата със сферата и главния меридиан на сферата. Равнината, определяща главния меридиан, пресича призмата по права линия, върху която трябва да бъдат разположени посочените точки. Чертежът показва развитието на призма. Кривата на размаха е изградена от дъги от кръгове. Радиусите за изчертаване на тези дъги се вземат частично от фронталната проекция (R2, R3, R4) и частично се намират с помощта на допълнителната проекция (R1 и R5).