Пряко и директно адресиране
Нека разгледаме два примера.
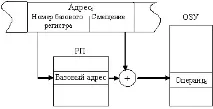
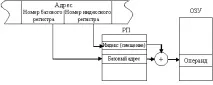
11.Законите на Амдал и Густафсон.
DOP (степен на паралелизъм)
Степента на паралелност на програмата - D(t) - броят на процесорите, участващи в изпълнението на програмата в момент t
DOP зависи от програмния алгоритъм, ефективността на компилацията и наличните ресурси при изпълнение
График D(t) - профил на програмен паралелизъм
T(n) – времето за изпълнение на програмата на n процесора
T(n) T(1), ако режийните разходи (разходите) за прилагане на паралелната версия на алгоритъма са прекалено високи
Ускорение поради паралелно изпълнение
Ефективност на система от n процесора
Случай S(n)=n - линейно ускорение - скалируемост (Scalability) на алгоритъма (способността за ускоряване на изчисленията е пропорционална на броя на процесорите)
Случай S(n)>n - свръхлинейно ускоряване (напр. поради по-висок коефициент на попадение в кеша)
Джийн Амдал (1967)
f е делът на последователната част на програмата
1-f - дял на паралелизираната част от програмата
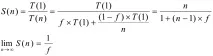

Практически граници на ускорението
Джийн Амдал формулира закона през 1967 г., след като откри ограничение, просто по същество, но непреодолимо по съдържание, за растежа на производителността при паралелни изчисления:
„В случай, че задачата е разделена на няколко части, общото време на нейното изпълнение в паралелна система не може да бъде по-малко от времето на изпълнение на най-дългия фрагмент.“ Ако споделената част от кода f може да бъде равномерно формално разпределена върху n процесора, тогава моделът може да бъде написан, както е показано на фиг. 1.

Законът определя теоретично възможна горна граница, но на практика ситуацията е още по-лоша - частресурсите на всеки процесор се изразходват за съвместна работа, а шините имат ограничена честотна лента.
Единственото известно предположение за възможността за преодоляване на описаните ограничения е направено през 1988 г. от Джон Густафсън, но то не се отнася за подгрупа от фиксирани проблеми. Въз основа на натрупания опит Gustafson стигна до извода, че когато изграждат по-мощни системи, потребителите са склонни да не намаляват времето за изпълнение на текущата версия на проблема, а да преминат към нова версия, която осигурява по-високо качество на решението:
S(P)= P - l(P - 1), където P е броят на процесорите, S е ускорението, l е частта от кода, която не може да бъде паралелизирана.
Закон за мащабирано ускорение:

Да предположим, че дадена структура може да бъде изчислена по метода на крайните елементи и в този случай колкото по-малък е размерът на елемента, толкова по-висока ще бъде точността. Днес идеите на Gustafson, свързани с подобряването на методите за комуникация между възлите, се изпълняват в Massively Parallel Technologies (MPT), където, между другото, работи и самият Амдал. Допустимо е да се каже, че тези методи позволяват да се преодолеят ограниченията на закона, наречен на негово име, но само косвено.
Принципът за замяна на прости задачи с по-сложни, предложен от Густафсон, е по-екзотичен от ежедневната практика, следователно в масовите приложения, на които разчитат многоядрените процесори, се прилага законът на Амдал.