Проектни натоварвания и техните комбинации
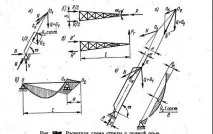
Общите разпоредби на проектните натоварвания и техните комбинации за стрелови и мачтови кранове с общо предназначение са дадени в таблица. 3 и 4. Теглото на метални конструкции без решетъчни глави на стрелата и мачти с квадратно или триъгълно сечение със странични размери 500 - 1000 mm е 1 - 2 kN / m. За да се определи хоризонталната сила в края на стрелата по време на работата на механизма за въртене, масатаmm, намалена до края му, се приема равна наml/3, къдетоmе масата на единица дължина на стрелата (фиг. 99,а). За веригата, показана на фиг. 99,b, от условието за равенство на кинематичната енергия в процеса на свободни трептения на равномерно разпределената маса на стрелкатаmи масатаmm, намалена до нейния край, намираме, че
,
къдетоωе ъгловата скорост на стрелата. Оттук
mm = .
Експлоатационните натоварвания и техните изчислени комбинации зависят от вида на крана и неговите работни условия и се изследват за серийно произвеждани кранове.
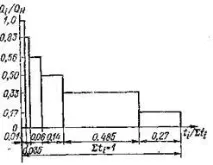
| Фигура 100 - Обобщен график за поетапно натоварване за автокранове с товароподемност 4; 6.3; 10 и 16т. |
Фигура 99 - Схеми за проектиране на стрелки
На фиг. 100 показва шестстепенна графика на относителната величина на натоварването върху куката на автокранове, която е записана от оборудването, без да се отчита динамиката, т.е. беше изключено влиянието на вида на задвижването и методите на работа на краниста. Съгласно тази графика, подобно на формула (166), къдетоРi=Qi, иРН=Qи вместо относителния брой циклиZi/ΣZiсе взема относителното време на работаti/Σti, формулата за изчислениеима формата
и коефициентите на еквивалентностφeимат следните стойности: 0.44 приm= 3; 0,48 приm= 4 и 0,55 приm= 6. Площите на разпределение на натоварването върху металните конструкции на стрелите на плаващи кранове в речни пристанища с товароподемност 10 и 15 тона, получени при експлоатационни тестове, показаха, че напреженията в стрелите се разпределят по нормални закони, стойността на средното напрежение се дължи на теглото на стрелата и стойността на максималното напрежение (минимално напрежение) в цикъла е сумата от средното напрежение и напреженията, причинени от максимални (минимални) стойности на външни натоварвания.
Характеристики на изчислението
Общи въпроси за изчисляване на компресирани и компресирани извити елементи както с призматично, така и с променливо напречно сечение по дължина, както и изчисления на несвързани и пространствени ферми са разгледани в l.11. Обширна литература е посветена на определянето на критичното натоварване при загуба на стабилност на стрелите на крана в зависимост от променливостта на инерционния момент на сечението по дължината в равнината на окачване на стрелата и в хоризонталната равнина при условия на надлъжно-напречно огъване. В допълнение към сложността на такива изчисления, те освен това не отчитат напълно всички обстоятелства на работата на стрелките. Поради това, вместо да се проверява устойчивостта им, е препоръчително да се изчисли якостта им по деформационен метод (виж л.11). В този случай огъващите моменти и напречните сили в стрелата, възникващи в резултат на деформации, трябва да се определят както в равнината на окачване, така и от равнината на окачване. За решетъчните стрелки е необходимо да се определят техните деформации, което е много по-трудоемко от определянето на деформациите на стрелите на гредите, които в много случаи се изчисляват с помощта на готови формули. За да определите отклоненията на фермите, можете да използвате техниката, при която отклонениетоферма се определя като отклонение на еквивалентна греда. Деформацията на фермата се определя от деформациите както на хордите, така и на решетката. Инерционният момент на фермата, когато се разглежда като греда с еквивалентна твърдост, се определя въз основа на равенството на деформациите на фермата и гредата за дадените условия на закрепване и натоварване. Ако инерционният момент на фермата се дефинира като инерционния момент на нейните хордиJp, той ще бъде преувеличен и следователно деформацията ще бъде подценена. Преувеличаването на инерционния момент ще бъде толкова по-голямо, колкото по-малка е твърдостта на решетката. Като се вземе предвид деформацията на решетката, инерционният момент на ферматаJ=Jp / µ, където µ>gt; 1 е коефициентът, който отчита ефекта от деформацията на решетката. В много случаи µ ≤ 1,1. За стрела с права ос, най-голямата сила на натиск в колана
Влиянието на силата на налягането на вятъра върху наветрената повърхност на стрелата се взема предвид както обикновено. От действието на тежестта на стрелата възниква огъващ момент иMmax=G2lcos α/8. Влиянието на това огъване може да бъде значително намалено от момента с противоположен знакM0 =N'e, поради изместването на оста на повдигащия блок към точкатаO2 (фиг. 101,d). Ако подемното въже се прекара през пръстените, фиксирани на стрелата, така че да се огъва заедно със стрелата, напрежението във въжето няма да причини допълнително огъване на стрелата. Приa≈ 0,2lв обхвата и в точката на закрепване на теглещото въже към стрелатаO1, изчислените стойности на огъващите моменти ще бъдат същите (фиг.101,e). В равнината на окачване влиянието на теглото на стрелата може да бъде значително намалено чрез прилагане на сила на натискRс ексцентричностe, т.е. изместете оста на стрелата нагоре сепо отношение на линията, свързваща осите на крайните блокове и долните панти на стрелата (фиг.101,е). Акоe=G2l/ (25R), натоварването на срязване на отвесастрелата няма да повлияе на големината на критичната сила и стрелата може да бъде тествана за стабилност, без да се взема предвид огъването от нейното тегло, като централно компресиран прът.
Фигура 101 - Изчислителна схема на стрелка с права ос
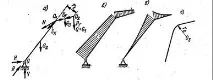
Фигура 102 - Изчислителна схема на стрелка с извита ос
За стрела с извита ос (фиг. 102,a) са дадени диаграми по дължината на стрелата на силите на натиск (фиг. 102,b) и огъващите моменти (фиг. 102,c) за случая, когато теглото на стрелата се разглежда като равномерно разпределено натоварване. Най-голямата компресия в основата на стрелката се причинява от реакциятаRспрямо посоката на стрелката. Хоризонтална силаPg, перпендикулярна на чертежа, приложена в точкаO2 (фиг. 102,a), в допълнение към допълнителните усилия в ремъците на стрелата (вижте фиг. 101,c), причинява усукване на долната част на стрелката до моментаMcr =Pgr1 (фиг. 102,a),, което е недостатък на този тип стрели. За стрели с извита ос (фиг. 102,g), характеристика на изчислението е определянето на напреженията в извитата част, които трябва да се извършват съгласно формулите за извита щанга. При избора на посоката на подемното въже по дължината на стрелата трябва да се има предвид, че ако въжето минава под оста на стрелата, силата във въжето намалява огъващия момент в стрелата от теглото му. Стрелките се изчисляват в няколко позиции, включително тези с най-голям и най-малък надвес. Най-натовареният клон на стрелата се проверява за стабилност. Проверката на общата стабилност на стрелата се извършва в равнината и от равнината на окачване по схемата на ексцентрично компресиран прът с ексцентричност в равнината на окачване, определена от отклонението от теглото на стрелата, и от равнината - от отклонението от инерционните сили при завъртане, от страничния вятър и накланяне.
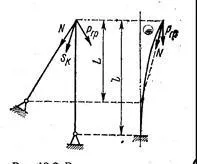
Фигура 103 -Схема за изчисление, като се вземе предвид ефектът на човека върху стабилността на стрелата.
В равнината на окачване прогнозната дължина на стрелата се определя като за прът с два шарнирни края и от равнината, като за прът с един вграден и другия свободен край. В последния случай влиянието на скобата подобрява стабилността на стрелата. Когато краят на стрелата напусне равнината на окачване, силата в елементаN,, която преди това е действала в равнината на окачване, става наклонена към нея, което предизвиква компонент на силата, който предотвратява отклонението на края на стрелата (фиг. 103). За изчисляване въвеждаме коефициентаk=Nl/(PL),къдетоР≈N + Рgr е общото натоварване на стрелата;N– сила на теглене на въже;Рgr – сила от товара. Коефициентътkсъответства на следните стойности на коефициента на намаляване на дължинатаµ(виж L.11), за случай на абсолютно твърда основа на стрелата и точките за фиксиране на скоби.
Съответствието на фиксиращите точки намалява критичното натоварване (в по-малка степен при наличието на скоба, отколкото при нейното отсъствие). Дадените стойности на µ показват, че приемането на прогнозната дължина на стрелкатаlcalc = 2l, както за прът с един вграден и друг свободен край, става само когатоL= ∞, т.е. когато няма ефект на издърпване. Приk= 1 (l=L)lcalc =l, т.е. и в двете равнини стрелата е прът с два шарнирни края. И накрая, приL= 0lcalc = 0.7lи стрелката в равнината, перпендикулярна на окачването, е прът с единия вграден и другия шарнирен край.
Изчисляването на стрелките на листата трябва да се извърши съгласно материалите, дадени в l. 11, пространствена решетка и bezraskosnyh.
Използвана литература: Основна: 6 [Разд. 19: стр.210÷219; раздел 18: стр.203÷210].
1. Какви са видовете конструкции на порталните кранове и дайте основните им параметри?
2. Дайте описание на изчислителните натоварвания и техните комбинации за металните конструкции на порталните кранове?
3. Какви са характеристиките на изчисляването на метални конструкции на портални кранове?
4. Какви са видовете метални конструкции на стрелови кранове?
5. Дайте описание на изчислителните натоварвания и техните комбинации за металните конструкции на стрелови кранове?
6. Дайте описание на изчислителните натоварвания и техните комбинации за металните конструкции на стрелови кранове?
7. Какви са характеристиките на изчисляването на метални конструкции на стрелови кранове?