Прогноза за вероятност за преобразуване
Автор: Андрей Белоусов, управляващ партньор на HTraffic.ru
За правилно офериране е важно да се изчисли възможно най-точно вероятността за реализация за всяка ключова дума. Въпреки това, при малък брой кликвания, процентът на реализация не може да се вярва - той има значителна грешка. В тази статия ще предоставя някои прости методи за подобряване на точността на вашата оценка на вероятността за реализация.
Вероятност
Не бъркайте процента на реализация с процента на реализация. Например, ако имаме 1 клик и 0 реализации, тогава индикаторът е нула, но това не означава, че вероятността за покупка също е нула.
Вероятността, по дефиниция, е честота в безкрайност. С други думи, ако броят на кликванията беше безкрайно голям, тогава процентът и вероятността за реализация биха били равни. При голям брой кликове тези две числа са приблизително равни. Но ако са малки, те могат да се различават значително.
Грешка
Благодарение на теорията на вероятностите е лесно да се изчисли средната грешка, която има процентът на преобразуване. Това число показва колко средно процентът на реализация се различава от неговата вероятност:
Къдетоpе вероятността за реализация,nе броят кликвания. Например при конверсия = 1% и 100 кликвания получаваме
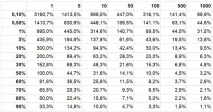
На пръв поглед това е малка грешка, но желаното число (вероятност за преобразуване) също е малко и според условията на примера е 1%. С други думи, при 100 клика грешката е приблизително равна на процента на реализация.
Следователно, за по-голяма яснота, нека преминем към относителната грешка, разделяйки грешката на вероятността за преобразуване. Получаваме 99,5%.
Формула за относителна грешка:
Можем да изчислим относителната грешка в зависимост от броя кликове и процента на реализация. Получаваме:

Лесно е да се види, че при малък брой кликвания грешката е просто астрономическа. С едно кликване и 1% реализация, относителната грешка е 995,0%. Тоест грешката е почти 10 пъти по-голяма от вероятността за преобразуване.
Всъщност това е оценка на грешката отдолу. В действителност грешката ще бъде по-висока, тъй като процентът на реализация може да бъде повлиян, например, от факта, че по чиста случайност всичките 5 кликвания на ключовата дума са се случили през нощта.
В статистиката е обичайно да се използва бета-биномен модел за оценка на вероятността. Той например се използва от Marin Software, според техния патент. Ние от К50 също използваме подобна схема.
Шанс за реализация ≈(Конверсии + A)/(Кликвания + A/M)
A— степен на обединяване, някакво число. Изразява степента на сходство на ключови думи в група.
Количеството обединяване е по същество количеството информация, която групата носи и която добавяме към информацията за ключовата дума. В статистиката А обикновено се измерва в псевдо-успехи или, в нашия случай, псевдо-конверсии. Съотношението A/M е броят на псевдо-наблюденията или, в нашия случай, псевдо-щракванията.
В резултат на това тази формула е лесна за запомняне:реализации + псевдореализации, разделени на кликвания + псевдокликвания.
Меко обединяване
Теоретичната оценка отдолу A=1. Това, което се потвърждава от практиката. С изключение на големите онлайн магазини, които продават всичко - от памперси до хладилници. Ако имат всичките си ключови думи като група, тогава оптималното А е около 0,7. И дори в този случай 0,7 е по-близо до 1, отколкото до 0. Следователно мекото групиране не е по-лошо от липсата на групиране изобщо.
В резултат на това нашата формула:
Вероятност за реализация ≈(Конверсии + 1)/(Кликвания + 1/M )
Друг пример: ключова дума има 10 кликвания и нито една реализация, резултате равно на (0+1)/(10+ 1/1%)=1/110=0,91%
За да разберем адекватността на този метод, ще изградим таблица:
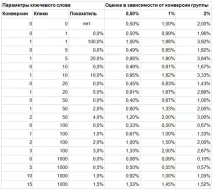
Както виждаме, оценките са доста адекватни. При малък брой кликвания резултатът е много по-добър от процента на реализация, при голям брой те са почти еднакви.
Можем да изчислим максималната грешка, която ще бъде с меко обединяване и да я сравним с грешката без обединяване:
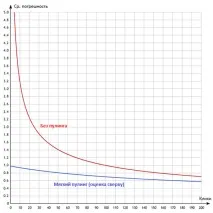
Обединяване на много нива
Тази връзка е таблица в Google Документи, която оценява вероятността от преобразуване с помощта на метод за обединяване на много нива. Копирайте го на вашия Google диск или го запазете като файл за Microsoft Excel.
Освен това е възможно да се изчисли оценка не само на вероятността за преобразуване, но също така, например, вероятността от неуспех. Просто трябва да замените броя на отпаданията вместо броя на реализациите.
Най-лесният начин за изчисляване на данни е за меко групиране. За да направите това, просто трябва да копирате данните за ключовите думи в таблицата.
Тази таблица също така взема предвид грешката, която можете да намалите, като изберете оптималната степен на обединяване. За да направите това, трябва да въведете статистика за два периода.
Като цяло, за да изберете степента на обединяване, трябва:
- Разделете данните на два периода, които не се припокриват. Например пролет и лято 2015 г. и вмъкнете тези данни в таблица.
- Опитайте да промените степента на обединяване „Ad->Keyword“ (H4). така че да се минимизира грешката (D9)
- Опитайте да промените нивото на обединяване „Кампания->Реклама“ (F4). така че да се минимизира грешката (D9)
- Опитайте да промените количеството на обединяването "Account-> Кампания“ (D4). така че да се минимизира грешката (D9)
- Върнете се към втората стъпка и преминете през този цикъл още няколко пъти. И в крайна сметка ще намеритеоптимални коефициенти на обединяване. Това може да отнеме до половин час, но за всеки сайт това трябва да се прави веднъж в живота.
- Въведете общи данни за целия период и таблицата ще изчисли сравнително точни оценки на реализациите.
Грешка (D9), дори и при идеална прогноза, никога няма да бъде нула. Факт е, че в контролния месец броят на кликванията не е безкрайно голям, но ние сравняваме нашата прогноза с процента на реализация на контролния месец, който отразява вероятността от реализация с много голяма грешка.
Следователно намаляването на грешката от, да речем, 40% на 36% ще повиши ефективността на залагането с много повече от 10%.
Регресионен анализ
Има цял раздел от математическата статистика, който изучава връзката между променливите и ви позволява да предвидите стойността на една променлива, като се имат предвид известните стойности на други. Този раздел се нарича "регресионен анализ".
Да приемем, че имаме конверсия от 1% и степен на отпадане от около 50%. Използвайки таблицата, дадена в началото на статията, можете да разберете, че грешката в степента на отпадане е 10 пъти по-ниска от тази в процента на реализация за същия брой кликвания.
Въпреки това, тези променливи са силно обратно корелирани. В зависимост от обекта - от 60% до 90%. Грубо казано, това означава, че можем да възстановим вероятността за преобразуване с точност от 60%-90%, знаейки вероятността от неуспехи.
Като цяло можем да намалим грешката при преобразуване няколко пъти, като добавим информация, която носи степента на отпадане.
Но за това трябва да изградите статистически модел. Благодарение на формулата за обща вероятност, можем да разширим вероятността за преобразуване, както следва:
P[преобразуване] — вероятност за преобразуване
P[failure] - вероятност за отказ
K— вероятностче преобразуването ще се случи, ако не е имало грешка.
За простота нека приемем, че K е някаква константа, която е еднаква за всички ключови думи. Това предположение може да изглежда доста грубо, но на практика дори такъв прост модел има доста висока точност.
Kможе да се оцени като:
Можем да оценим вероятността от неуспех, като използваме обединяване. Просто трябва да замените броя на отпаданията в таблицата вместо броя на реализациите. След това заместваме оценката на вероятността за отхвърляне в тази формула и получаваме друга оценка на конверсията. Нека го наречем резултат за отхвърляне.
Претеглен резултат
Оценката на неуспеха може да се комбинира с общата оценка. И по този начин да получим крайната оценка с грешка, по-малка от тази на две междинни оценки. Например така:
Краен_резултат = w * Обединен_резултат + (1-w) * Failure_score
Къдетоwе число от 0 до 1 и се избира по същия начин като степента на обединяване, чрез минимизиране на грешката в оценката. За да направите това, в същата таблица има втори лист. Можете да копирате две оценки там и да изберете w, за да минимизирате грешката.
Крайният резултат ще бъде по-добър от обединяването и по-добър от резултата за отпадане. Е, поне не по-лошо. Например, ако резултатът за неуспех е много лош, много по-лош от обединяването, тогава оптималното w ще бъде равно на 1. И крайният резултат ще бъде равен на резултата за обединяване.
Динамично претегляне
Проблемът с предишния метод е, че w не зависи от броя кликвания. Въпреки че резултатът за обединяване е по-точен за ключови думи с висока честота, а резултатът за отпадане е по-точен за ключови думи с ниска честота.
Взехме това предвид на четвъртия лист. Там също трябва да изберете само един коефициент -S, относителната систематична грешка на модела. Благодарение на първиялист, оценете вероятността за преобразуване чрез обединяване и копирайте оценката и нейната очаквана грешка върху четвъртия лист. Благодарение на първия лист, преценете вероятността от неуспех чрез обединяване и копирайте оценката и нейната очаквана грешка на четвъртия лист. Регулирайте настройката S, за да минимизирате среднопретеглената относителна грешка.
Модел на скрита повреда
Степента на отпадане е твърде ниска. Тъй като фактът, че потребителят е отишъл на втората страница, не означава, че се е интересувал от вашия продукт или услуга. Можеше да направи това от празно любопитство или без да разбере какво точно му се предлага.
Да предположим, че има някаква скрита степен на отпадане. Вероятност за фалшиво отрицателен брояч на грешки. Когато незаинтересован потребител дойде при вас и броячът на отпадания не идентифицира такъв потребител.
Като цяло: Степента на отпадане е занижена. Това се отразява на качеството на прогнозата. Можем да компенсираме този ефект чрез изграждане на модел. Параметрите на модела могат да бъдат избрани така, че качеството на прогнозата да е възможно най-високо.
Очевидно е, че колкото повече са явните провали, толкова по-скрити трябва да са тези. От друга страна, като всяка друга вероятност, вероятността за скрит отказ трябва да бъде по-малка от 1. Следователно може да се изгради следният модел:
P[латентна повреда] = erf(L * P[повреда])
КъдетоLе някаква положителна константа. Аerfе функцията за грешка. Винаги е по-малко от 1. Тази функция е в Excel.
В резултат на това получаваме:
Вероятност за реализация = K * (1 - P[Отхвърляне]) * (1-erf(L * P[Отхвърляне]))
КъдетоKиLса избрани по начина, който вече знаем, за да минимизираме грешката. Първоначалното K може да бъде взето от предишния метод и като първоначално използвайте L =0,5. За да направите това, масата има трети лист.
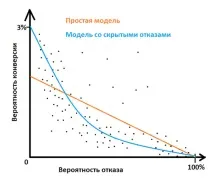
Моделът на скрития отказ описва реалните данни доста добре. Има само два параметъра. Практиката показва, че този модел работи също толкова добре, колкото моделите, базирани на полином с 4-6 параметъра.
Претегляне на обратната дисперсия
Ето последната схема за сравнително точна оценка на конверсията: Обмислете обединяването (първия лист) като оценка на конверсията и копирайте оценката и грешката на четвъртия лист. Ние считаме обединяването (първия лист) за оценка на вероятността от неуспех. Копираме грешката на четвъртия лист и оценката на третия лист. Преброяваме третия лист и копираме общата вероятност от неуспехи в четвъртия лист като оценка на вероятността от неуспехи. Преброяваме четвъртия лист и получаваме доста точна оценка на вероятността за преобразуване.
Заключение
Тази схема е най-точната от тези, които могат да се изчислят ръчно без специфични познания по математическа статистика.
Автоматизираните системи като K50 и Marin Software използват малко по-сложни схеми за обединяване, но без елементи на регресионен анализ. Качеството на тяхната прогноза вероятно ще бъде по-високо от това на тази схема, но не много. Всички тези системи спестяват много време и елиминират човешки грешки.
