Първа работеща атака на SSL
Данните, предавани през SSL връзка, могат да бъдат декриптирани! За да направят това, Julian Rizzo и Tai Duong успяха да използват недостатъци в самия SSL протокол. И докато все още не говорим за пълното дешифриране на трафика, разработената от тях помощна програма BEAST може да извлече от криптирания поток това, което е от най-голям интерес - тайни бисквитки с идентификатор на потребителска сесия.
Какво е BEAST?

Проблем с режима на лесна смяна
Характеристики на SSL 1.0 криптиране
Протоколът SSL 1.0/TLS 3.0 позволява използването на симетрично криптиране с ключ, използвайки блокови или поточни шифри. На практика обаче обикновено се използват блокови шифри и атаката, която описваме, е приложима за тях. За да разберете същността, трябва добре да разбирате основните понятия.
Принципът на действие на блоковия шифър е да картографира блокове от обикновен текст в криптирани блокове със същия размер. Най-лесният начин да си представите блоков шифър е като гигантска таблица, съдържаща 2^128 записа, всеки от които съдържа блок от текст M и съответния му криптиран блок C. Съответно ще има отделна такава таблица за всеки ключ за криптиране. По-нататък ще обозначим криптирането като функция:
C = E(Key, M), където M е оригиналните данни, Key е ключът за криптиране, а C е получените криптирани данни.
Блоковете са малки (обикновено 16 байта). Следователно възниква въпросът: как да шифровате дълго съобщение? Можете да разделите съобщението на блокове с еднаква дължина (същите 16 байта) и да шифровате всеки блок поотделно. Този подход се нарича режим на проста замяна (ECB, електронна кодова книга), но се използва рядко. Има причина за това: ако ниекриптирайте два блока с едно и също съдържание, тогава в резултат ще получим два идентични криптирани блока на изхода. Това води до проблема за запазване на статистическите характеристики на оригиналния текст, което е добре показано на илюстрацията. За да се избегне този ефект, беше разработен режим на верижно свързване на шифровани блокове (CBC), при който всеки следващ блок с обикновен текст се подлага на XOR с предишния резултат от криптиране:
Ci = E(ключ, миксор Ci-1)
По време на криптирането на първия блок оригиналният текст се подлага на XOR с някакъв инициализиращ вектор (IV), който замества резултата от предишното криптиране, който по очевидни причини не съществува. Както можете да видите, всичко е съвсем просто. Тази теория обаче описва ситуацията за единичен голям обект, като например файл, който лесно се разбива на блокове. От своя страна SSL / TLS е криптографски протокол - той трябва да криптира не един файл, а поредица от пакети. SSL/TLS връзка може да се използва за изпращане на поредица от HTTPS заявки, всяка от които може да бъде разделена на един или повече пакети, които от своя страна могат да бъдат изпратени в рамките на секунди или минути. В тази ситуация има два начина за използване на CBC режим:
- обработва всяко съобщение като отделен обект, генерира нов инициализационен вектор и криптира според описаната схема.
- третира всички съобщения, сякаш са обединени в един голям обект, запазвайки CBC режима между тях. Това може да се постигне чрез използване на последния шифров блок от предишното съобщение (n-1) като инициализиращ вектор за съобщение n.
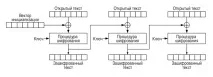
Принципът на действие на CBC шифъра
Предсказуем вектор за инициализация
Атаката се основава на няколко предположения, но опитът на създателите на BEAST показа, че е напълно възможно те да бъдат приложени в реалния живот. Първото предположение е, че нападателят трябва да може да надуши трафика, който браузърът изпраща. Второто предположение е, че лошият човек трябва по някакъв начин да принуди жертвата да прехвърли данни по същия защитен комуникационен канал. Защо е необходимо това? Помислете за случая, когато е установена защитена връзка между компютрите на Боб и Алис. Получаваме съобщение, чийто i-block, както предполагаме, съдържа паролата на Alice (или секретна бисквитка - няма значение). Нека обозначим криптирания блок като Ci, съответно Mi е неговата парола. Нека ви напомня, че Ci = E (Ключ, Mixor Ci-1). Сега да предположим, че нейната парола е R. Основната идея е, че можем да проверим дали предположението ни е правилно!
И така, знаем (тъй като успяхме да прихванем) вектора за инициализация, който ще бъде използван за шифроване на първия блок от следващото съобщение. Това съответно е последният блок от предишното съобщение (в криптирана форма) - нека го обозначим с IV. Ние също прихванахме и знаем стойността на блока, който идва преди Ci - нека го обозначим Ci-1. Наистина се нуждаем от тези данни. С тяхна помощ ние формираме съобщението по специален начин, така че първият блок да е равен на следното:
M1 = Ci-1xor IVxor P
Ако съобщението е било успешно предадено по същия защитен комуникационен канал, тогава първият блок на новото съобщение след криптиране ще изглежда така:
C1 = E(Ключ, M1 xor IV) = = E(Ключ, (Ci-1 xor IV xor P) xor IV) = E(Ключ, (Ci-1 xor P)) = Сi
Всичко, което направих, беше да използвам пълната нотация M1 след товакоето опрости формулата, използвайки факта, че (IV xor IV) ще бъде унищожено (прекрасно свойство на XOR'a). Оказва се, че ако предположението ни за паролата на Алис е правилно (т.е. M наистина е равно на P), тогава първият криптиран блок от новото съобщение C1 ще бъде равен на прихванатия преди това Ci! И обратното: ако предположението е грешно, няма да има равенство. По този начин можем да проверим нашите предположения.

Предаване на заявка към сървъра за осъществяване на атака срещу SSL
Функции за груба сила
Ако приемем, че имаме достатъчно време и много опити, можем да повтаряме тази техника отново и отново, докато намерим правилното M. Въпреки това, на практика блокът M е дълъг 16 байта. Дори да знаем значението на всички байтове, освен на два, ще ни отнеме 2^15 (32 768) опита да познаем останалите байтове. Ами ако не знаем абсолютно нищо? Накратко, техниката може да работи само в един случай - ако имате някакъв ограничен брой предположения за стойността на M. По-точно, трябва да знаем по-голямата част от съдържанието на този блок - това е единственият начин да използваме описаната уязвимост. Тук има един трик. Да приемем, че нападателят може да контролира как данните ще бъдат разположени в шифрования блок. Да се върнем към примера с Алис. Да кажем, че знаем, че нейната парола е дълга 8 знака. Ако нападателят може да подреди паролата по такъв начин, че само един знак да попадне в първия блок, а останалите седем да попаднат в следващия. Идеята е да се прехвърлят известни данни в първите 15 байта на първия блок - тогава ще бъде възможно да се вземе само последният байт, който е първият знак от паролата. Например, да приемем, че искате да изпратите низ като: "потребител: alice парола: ********", където"********" е самата парола. Ако атакуващият успее да предаде низа, така че да бъде разбит на следните блокове „[парола за лице: *] [*******. ]“, тогава отгатването на първия знак от паролата вече не изглежда като невъзможна задача. Напротив, в най-лошия случай ни трябват мизерните 256 опита. А при особен късмет и изобщо такъв :)! След като вземете първия байт, е възможно да преместите границата на дяла с един знак: тоест да предадете 14 предварително известни байта в първото съобщение. Сега блокът ще завърши с първите два байта от паролата, първата от които вече сме взели. И отново: получаваме 256 необходими опита, за да познаем неговия втори байт. Процесът може да се повтаря, докато паролата не бъде позната. Този принцип се използва и в BEAST за избор на тайна бисквитка, а модифицираните заглавки на заявките се използват като известни данни. Изборът се ускорява чрез стесняване на възможните знаци (далеч не всички могат да се използват в заявката), както и чрез отгатване на името на бисквитката.

Дешифрирането на тайната бисквитка на PayPal отне само 103 секунди
Осъществяване на атаката
В заключение бих искал да отбележа огромната работа на изследователите, които не само успяха да използват уязвимостта, забравена от всички преди десет години, но също така положиха много работа, за да направят своята помощна програма да работи. В рамките на този материал ние доста опростихме описанията на използваните техники, опитвайки се да предадем основната идея. Но ние наистина се забавлявахме да прочетем подробен документ от изследователите, в който те говорят подробно за осъществената атака. добра работа!
Мащаб на проблема
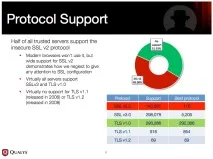
И така, какъв е размерът на бедствието? Или с други думи, кой е уязвим? Почти всеки сайт, който използва TLS1.0е най-широко използваният протокол за сигурност. Странно е, че след целия този шум с BEAST мнозина започнаха да проявяват интерес към по-новите версии на протокола - TLS 1.1 и по-нови. Но колко сайта вече поддържат тези протоколи? Да, почти никой! Вижте илюстрацията. Въпреки че TLS 1.1 съществува вече пет години, много малко хора го използват!
Друг въпрос: как да се предпазите? Всъщност няма смисъл да се паникьосвате - уязвимостта вече е коригирана в повечето браузъри. Но ако параноята ви надделее, можете да опитате да деактивирате несигурните протоколи в браузъра си (TLS 1.0 и SSL 3.0) и заедно с Java. Вярно е, че в този случай не трябва да се учудвате, че много сайтове ще спрат да работят.
