Работа със статистически данни с помощта на електронни таблици
Урок 1
1. Задачи по математическа статистика
„Статистиката знае всичко” - с тези думи започва втората част от романа на И. Илф и Е. Петров „Дванадесетте стола”. „Известно е колко храна изяжда средният гражданин на републиката годишно ... Известно е колко ловци, балерини ... машини, кучета от всички породи, велосипеди, паметници, момичета, фарове и шевни машини в страната.
Колко живот, пълен с плам, страсти и мисли, ни гледа от статистическите таблици!” Защо са необходими тези таблици, как да се съставят и обработят, какви изводи могат да се направят от тях - на тези въпроси отговаря статистиката (от италиански stato - състояние, лат. status - състояние).
Съвременната математическа статистика се определя катонаука за вземане на решения при несигурност.Има две основни задачи на математическата статистика:
- Посочете методите за събиране и групиране на статистическа информация, получена в резултат на наблюдения или в резултат на експерименти.
- Разработване на методи за анализ на статистически данни в зависимост от целите на изследването. В тази връзка се извършва следното:
- оценка: неизвестна вероятност за събитие, неизвестна функция на разпределение, параметри на разпределение, зависимост на случайна променлива от една или повече случайни променливи.
- проверка на статистически хипотези за формата на неизвестното разпределение или за големината на параметрите на разпределението.
И така, задачата на математическата статистика е да създаде методи за събиране и обработка на статистически данни за получаване на научни и практически изводи.
2. Генерална и извадкова популация
Извиква се набор от проби (проба)набор от произволно избрани обекти.
Генералната съвкупност(GS) е съвкупността от обекти, от които е направена извадката.
Размер на колекцията– броят на обектите в тази колекция.
Например: от 1000 части се избират 100, след това Вг.с. = 1000, Vv.s. = 100.
3. Многократно и еднократно вземане на проби. Представителна извадка
При съставянето на извадка може да се процедира по два начина: след като обектът е избран и наблюдаван върху него, той може да бъде върнат или не върнат в генералната съвкупност. В първия случай пробата се нарича повторна, във втория - неповторена. Извадката трябва правилно да представя пропорциите на генералната съвкупност - да бъдепредставителна(представителна).
4. Методи за подбор
Избор, който не изисква разделянето на HS на части:
Селекция, в която GE е разделена на части:
5. Статистическо разпределение на извадката
1. Да предположим, че в резултат на някакъв експеримент е получена пробаx1, x2, x3. xn.
Ако всичкиxiса различни, тогава, като ги поставим във възходящ ред, получаваме вариационна серия.
Пример.Дадена е извадка: 13, 1, 15, 12, 11, 14, 2, 5, 6, 17, 25, 3, 4, 8, 10. Изградете вариационна серия.
Алгоритъм за решаване:
- Въведете оригиналните данни в таблицата.
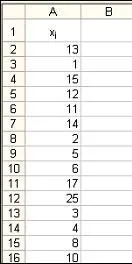
- Сортирайте елементите на първата колона във възходящ ред.
2. Нека се вземе проба от ХС иx1се наблюдаваn1пъти,
x2наблюдаваноn2пъти, ……………………….xkнаблюдаваноnkпъти.xiсе наричат варианти, а вариантът на последователността, написан във възходящ ред, се наричасерия от варианти;
niсе наричат честоти, и
ni = n –размер на извадката; (1)
wi =са относителни честоти и (2)
wi= 1. (3)
Статистическото разпределение на извадкатасе отнася до списъка с опции и съответните им честоти или относителни честоти.
3. Както от образецx1, x2, x3. xnда получи статистическото му разпределение (т.е. да изчисли честотите)?
Пример 1.Дадена е проба 1, 1, 1, 4, 3, 1, 5, 2, 2, 4, 4, 5.
Запишете статистическото разпределение на извадката.
1. Въведете първоначалните данни в таблицата.
2. Определете минималните и максималните стойности на функцията с помощта на функциите MIN и MAX.
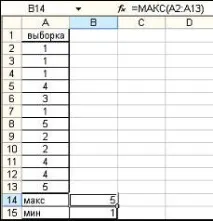
3. Компилирайте масив от интервали, в които е групиран масивът от данни, за които се изчисляват честотите (1, 2, 3, 4).
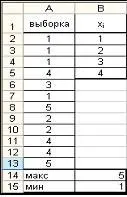
4. Определете честотите с помощта на статистическата функция FREQUENCY (за да се запише честотният масив в таблицата, трябва да изберете определен брой клетки и след извикване на функцията FREQUENCY, натиснете клавиша F2 и след това Ctrl + Shift + Enter).
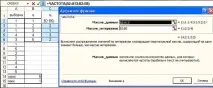
5. Така получаваме статистическото разпределение на извадката.
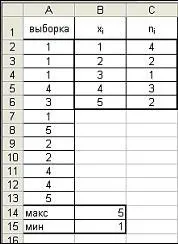
Пример 2.Нека е дадено статистическото разпределение