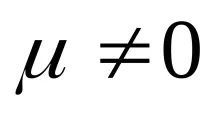Равномерна (хомогенна) деформация
Равномерна (хомогенна) деформация
Най-простият вид пластична деформация е равномерната (хомогенна) деформация.
Деформацията се нарича равномерна, ако компонентите на тензора на деформацията не са функция на координатите.
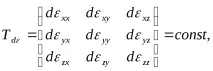
тоест деформациите са равномерно разпределени по целия обем на тялото.
Равномерната деформация е следствие от равномерното напрегнато състояние на тялото и може да се осъществи както в линейни, така и в равнинни и обемни схеми на напрегнатото състояние.
При равномерна деформация компонентите на движещите се точки
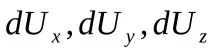
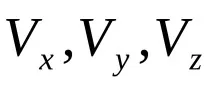
При равномерна деформация всички равнинни секции, начертани мислено в тялото преди деформацията, остават плоски след деформацията.
На практика е възможно да се получи равномерно напрегнато състояние само при специални условия.
В изследванията беше доказано теоретично и експериментално потвърдено, че при идеални условия на утаяване на тела между плоски успоредни плочи, т.е. при
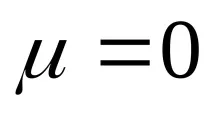
Степента на приближаване на деформацията до равномерна зависи от степента на приближаване на силите на контактно триене до нула.
В реални условия има нехомогенно напрегнато състояние и съответно неравномерно разпределение на деформациите по обема на тялото.
Въпреки това, определянето на деформираното състояние на тялото, като се вземат предвид всички характеристики на реалния процес на деформация, често среща големи трудности.
В тези случаи трябва да се прибегне до замяна на реалния процес с по-проста схема.деформации.
При решаването на някои специфични задачи вместо действителната неравномерна деформация се използва частична или пълна схема на равномерна деформация.
Това може да се направи, доколкото е възможно да се пренебрегне неравномерността на деформациите по посока на някои координатни оси.
Трябва да се има предвид, че когато реална неравномерна деформация е напълно или дори частично заменена от равномерна схема на деформация, не само разпределението на деформациите по обема на тялото се променя, но и граничните условия също се променят значително.
Така например зоната на залепване не се намира в схемата на равномерна деформация. По цялата контактна повърхност металът се движи спрямо инструмента.
При определяне на деформираното състояние на тялото въз основа на еднаква схема на деформация не могат да бъдат разрешени тези въпроси, които са следствие от неравномерна деформация.
Например, теоретично изследване на формата на цевта по време на тягата на цилиндри с умерена височина е невъзможно, когато се използва схемата за независимост на компонента на радиалното изместване
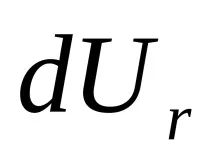
Следователно, когато се разглежда този въпрос, компонентите на тензора на деформация във всяка точка от обема на цилиндъра се представят като функция на две координати и елементите на еднакво напрежение не се използват в това изследване.
Следователно, когато е необходимо по-точно решение на проблема или решаване на въпроси, свързани с неравномерността на деформацията, е необходимо въз основа на експериментални данни да се избере схема на потока на метала, по-близка до реалната.
В зависимост от целите на конкретното теоретично изследване се решава въпросът за допустимостта на някои опростяващи допускания.
В заключение трябва да се отбележи, че пластичността на метала, при равни други условия,условия до голяма степен зависи от състоянието на напрежение, по-точно от разпределението на напреженията върху обема на тялото.
Експерименталните данни убедително доказват, че колкото по-близо е напрегнатото и следователно деформираното състояние до хомогенно състояние, толкова по-висока е пластичността на металите и техните сплави.
В някои случаи знакът на напреженията също е важен.
В случай на пластична деформация на нископластични сплави, тези факти трябва да се вземат предвид при разработването на технологични процеси.
Нека по-нататък разгледаме решението на обратната задача за вече известните процеси на MMD - пресоване на паралелепипед и цилиндър, ковашка протяжка, коване, валцуване, изтегляне и пресоване.
Освен това проблемите с търкалянето, изтеглянето и пресоването ще се считат за проблем с разстройването.
Този подход е напълно оправдан, тъй като пластичната деформация (или промяна на размерите) по една координата е следствие от компресия по друга координата (височина, дебелина или диаметър).
Първоначално проблемът се разглежда при липса на триене (
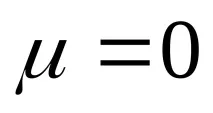
Резултатът от решението се използва като база при избора на функция на преместване за задача с реално триене (
