Разпределение на Уейбул
Разгледайте разпределението на Weibull, изчислете неговото математическо очакване, дисперсия, медиана. С помощта на функцията на MS EXCEL WEIBULL.DIST() начертаваме функцията на разпределението и графиките на плътността на вероятността. Нека генерираме масив от произволни числа и оценим параметрите на разпределението.
Разпределението на Weibull зависи от 2 параметъра: α (алфа)> 0 (определя формата на разпределението) и b (бета)> 0 (определя мащаба). Плътността на вероятността на това разпределение се дава по следната формула:
Ако параметърът алфа = 1, тогава разпределението на Weibull се превръща в експоненциално разпределение. Параметърът бета обикновено се приема >=1 на практика.
Функцията на разпределение се дава със следната формула:
Математическото очакване и дисперсията на разпределението се дават от следните изрази:
където Г(r) е гама функцията:
ако r е положително цяло число, то Г(r)=(r-1)!
Разпределението на Weibull е адекватен модел за описание на продължителността на работа на много технически устройства:
- време на повреда при износване. Повредата трябва да възникне поради повреда на най-малко надеждния компонент (принцип на най-слабата връзка);
- време на повреда на материала поради разрушаване (якост на материала). Повредата трябва да се дължи на вътрешен дефект. Ако параметърът алфа = 1 (експоненциално разпределение), тогава причината за повредата трябва да е външна причина.
Разпределение на Weibull в MS EXCEL
В MS EXCEL, започвайки от версия 2010, за разпределението на Weibull има функция WEIBULL.DIST(), английското име е WEIBULL.DIST(), което ви позволява да изчислите плътността на вероятносттаи кумулативната функция на разпределение (вероятността случайна променлива X, която има разпределение на Weibull, да приеме стойност, по-малка или равна на x).
Забележка : Преди MS EXCEL 2010, EXCEL имаше функцията WEIBULL(), която ви позволява да изчислите кумулативната функция на разпределение и плътността на вероятността. WEIBULL() е оставен в MS EXCEL 2010 за съвместимост.
Функционални графики
Примерният файл съдържа графики на плътността на разпределение на вероятностите и кумулативната функция на разпределение за няколко алфа и бета параметъра.
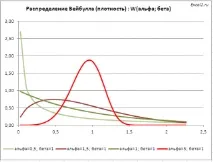
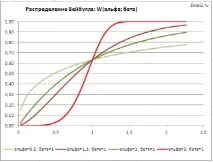
Разпределението на Weibull има обозначението Weibull(алфа; бета) или просто W(алфа; бета).
Забележка : За удобство при писане на формули в примерния файл са създадени съответните имена за параметрите на алфа и бета разпространение.
Примерният файл също изобразява плътността на вероятността и функциите на разпределение с маркирани средни, медиани и стойности на режима.


Генериране на произволни числа и оценка на параметри
Ние използваме обратната функция на разпределение (или p-квантил, вижте статията за квантилите), която за разпределението на Weibull може да бъде изразена изрично с помощта на елементарни функции:
Използвайки тази функция, можете да генерирате стойности на случайна променлива, която има разпределение на Weibull. За да направите това, използвайте формулата на MS EXCEL:
Функцията RAND() генерира непрекъснато равномерно разпределение от 0 до 1, което точно съответства на обхвата на вероятностната промяна (вижте примерния файлов лист Generation).
Сега, като имаме масив от произволни числа, генерирани с дадените алфа и бета параметри на разпределение (нека бъдат 200), нека оценим параметрите на разпределението.
Може да се направи оценка на алфа и бета параметриизползвайки линейна регресия. За да направите това, е необходимо да приведете функцията на разпределение на Weibull до формата на обикновена права линия, дадена от уравнението Y=aX+b. За да направим това, ще направим следните трансформации:
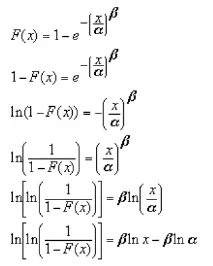
Сравнявайки израза с уравнението на правата Y=ax+b получаваме, че:
- Y съответства на лявата страна на израза,
- X - съответства на ln(x),
- параметърът на разпределението бета съответства на коефициента a, който е отговорен за наклона на правата спрямо оста x.
- изразът –beta*ln(alpha) съответства на коефициента b (ординатата на пресечната точка с оста Oy).
Всъщност ние практически изградихме вероятностна диаграма за разпределението на Weibull: ако сортираните стойности на ln(x), нанесени по оста Ox, лежат приблизително по права линия, това ще означава, че примерните стойности са взети от разпределението на Weibull. Остава да се модифицира оста Oy по формулата =LN(-LN(1-Ui)), където Ui=(i-0.5)/200 и i=1; 2; . ; 200.
Имайте предвид, че -LN(1-Ui) е обратната функция на разпределение с параметри алфа=1 и бета=1. Имахме нужда от втория логаритъм, защото абсцисата показва не самите x, а ln(x).
Забележка : Тъй като формата на разпределението на Weibull по същество зависи от неговите параметри, тогава вместо алфа=1 и бета=1 за обратната функция е по-добре да се използват точкови оценки на тези параметри, получени от извадката. Вижте по-долу как да изчислите алфа и бета оценки.
В примерния файл, на листа Generation, е изградена съответната вероятностна графика.

С помощта на функцията SLOPE() изчисляваме наклона на получената крива (коефициента на правата линия a, английски наклон), който служи като оценка на бета параметъра.
Функцията INTERCEPT() ще върне ординатата на пресечната точка с Oy (коефициента на правата b). Изразяване=EXP(-b/бета) служи като оценка на алфа параметъра.
След като изградим честотна хистограма въз основа на данните от извадката, ние я сравняваме с плътността на вероятността на разпределението на модела, т.е. разпределението, чрез което са генерирани самите стойности на извадката. Поради наличието на случайна грешка при вземане на проби (грешка при вземане на проби), стойностите могат да се различават.
Процедурата за конструиране на моделно разпределение е следната:
- Стойностите на плътността на вероятността на разпределението на модела се изчисляват като Pi - Pi-1, където P са стойностите на интегралната функция на разпределение в границите на интервалите на хистограмата, adx=1. (Обикновено плътността на вероятността на непрекъснато разпределение се изчислява като производна на функцията на разпределение dP/dx).
- В резултат на тази трансформация преминахме от непрекъснато разпределение към дискретно. Трябва да се уверите, че сумата от плътностите на вероятността е равна на 1.
- След като нормализирахме модифицираните плътности на вероятността по броя на стойностите в извадката (200), изчисляваме честотата на разпределението на модела за всеки интервал (можете да направите без нормализиране, като използвате спомагателната ос на диаграмата).
В резултат на това получаваме:

Както може да се види от диаграмата по-горе, съвпадението между разпределението на модела и примерната хистограма е доста добро.
Можете също така да сравните плътностите на вероятностите на разпределението на модела и разпределението с параметрите, получени от оценката.
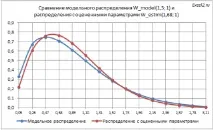
Както можете да видите от диаграмата по-горе, съвпадението също е доста добро.
СЪВЕТ : произволни числа се генерират с помощта на функцията RAND(), след което чрез натискане на клавишаF9 можете всеки път да получавате нова извадка и съответно нова оценка на параметрите.
СЪВЕТ : Можете да прочетете за други дистрибуции на MS EXCEL в статиятаРазпределение на случайна величина в MS EXCEL.