Развиваеми линейчати повърхнини - Студопедия
Правили се наричат повърхности, образувани от движението на права линия по определен закон.
Разгъваеми (торзални) са повърхности, които могат да бъдат разгънати в равнина без гънки или счупвания. Развиваемите линейни повърхности включват: цилиндрични; призматичен; коничен; пирамидален. Тези линейни повърхности имат един водач.
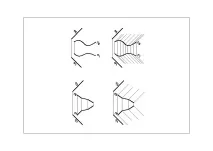
1.Цилиндрична повърхност Г (n, s ) (фиг.19)
(n, s ) – повърхностна детерминанта. Съдържание на детерминантата:n – водач (крива линия);
s – посоката на образуващата (образуващата е права линия).
Закон за образуване на повърхността (закон на Каркас):l i xn ;l i IIs.
2.Призматична повърхност L (n, s ) (фиг.20)
(n, s ) – повърхностна детерминанта. Съдържание на детерминантата:n – водач (прекъсната линия);
s – посоката на образуващата (образуващата е права линия).

3.Конична повърхност D (n, S ) (Фиг.21)
(n, S ) – повърхностна детерминанта. Съдържание на детерминантата:n – водач (крива линия);
S – повърхностен връх.
Закон за образуване на повърхността:l i xn ;l i Ìs.
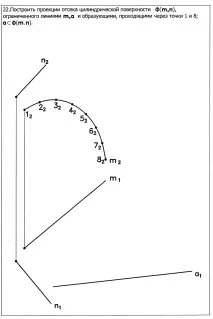
4.Пирамидална повърхност V (n,S ) (Фиг.22)
(n, S ) – повърхностна детерминанта. Съдържание на детерминантата:n – водач (прекъсната линия);
Закон за образуване на повърхността:l i xn ;l и МS.



Въпроси за самопроверка.
1. Какъв е начинът за формиране на повърхност в дескриптивната геометрия?
2. Дефиниране на образуваща.
3. Дайте понятието повърхностна детерминанта.
4. Определете закона за образуване на повърхността.
5. На каква основа се класифицират повърхностите?
6. Избройте основните класове повърхности, използвани в инженерството.
7. Как може да се уточни повърхност на сложен чертеж?
8. Какви са признаците за принадлежност на точките и линиите на повърхнината?
9. Какви повърхности са линейчати повърхности?
10. Задайте детерминантите и закономерностите на формиране на всички разгръщащи се повърхнини. Покажете техните прилики и разлики.
11. Коя от линейчатите разгърнати повърхнини може да заеме издадено положение?
Повърхности на въртене:
Всички повърхности на въртене се образуват чрез въртене на някаква образуваща около определена ос. Формата на повърхността на въртене се определя от формата на генератора и нейното местоположение спрямо оста.
Съставът на детерминантата на всяка повърхност на въртене (i ;l );
къдетоi е оста на въртене;l е образуваща.
Законът за образуване на повърхността на въртенеl Οi.
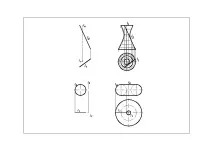
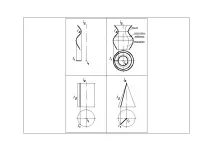

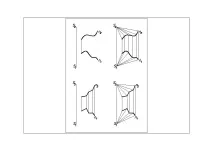
Цилиндрична повърхнина на въртене D (i,l ) (Фиг.26) [образуващата (правата) е успоредна на оста на въртене] Тази повърхнина "носи" две семейства прави, удобни за построяване на прави: 1. образуваща - прави; 2. концентрични окръжности с постоянен радиус - прави, лежащи в равнини, перпендикулярни на остаi.
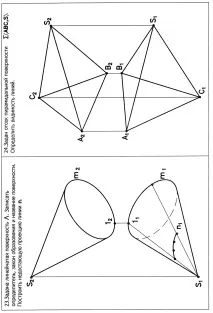
Конична повърхност на въртене L (i,l ) (Фиг.27)образуващата се пресича с оста на въртене(l xi ]
също "носи" две семейства прави, удобни за построяване на прави: 1. образуващи - прави; Ориз. 26 Фиг. 27 Фиг. 28 2. концентрични окръжности с променлив радиус (лежат в равнини, перпендикулярни на оста на въртене).
Еднослоен хиперболоид на въртене W (i,l ) (фиг.28) [(образуващата се пресича с оста на въртене (l -- i )] Има три семейства линии, удобни за конструиране на линии върху тази повърхност. 1. Две семейства образуващи (две пресичащи се прави линии с наклон в противоположни посоки и под един ъгъл към равнината, перпендикулярна на оста на въртене) 2. Концентрични окръжности с променлив радиус (лежат в равнини, перпендикулярни на оста на въртене.) АкоI ^ П 1, челното очертание на еднослоен хиперболоид на въртене ще бъде хипербола.

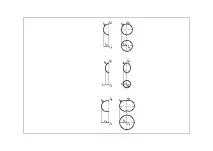


Сфера (фиг.29) Оста на въртене съвпада с диаметъра на кръга. Получената повърхност -сфера "носи" три семейства концентрични окръжности с променлив радиус. лежащи в равнини, успоредни на проекционните равнини.
Tor (фиг.30) Оста на въртене не минава през центъра на окръжността.Тори, фиг. 29 Фиг.30 Фиг.31 Фиг.32 показани на Фиг.30 се наричат затворени. На затворени тори има едно семейство от концентрични окръжности с променлив радиус, разположени в равнини, перпендикулярни на осите на въртене.
Пръстен (отворен торус) (фиг.31) Оста на въртене минава извън кръга. При пресичане на пръстена с равнини, перпендикулярни на неговата осi, получаваме две семейства концентрични окръжности с променлив радиус. Те могат условно да бъдат наречени семейства от вътрешни и външни кръгове на пръстена. .
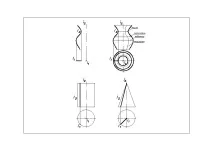
Образува се по време на въртенето на всяка линия, както плоска, така и пространствена, около фиксирана ос. Всяка точка от образуващата по време на въртене описва окръжност, лежаща в равнина, перпендикулярна на оста на въртене и с център, лежащ върху оста на въртене. Получените кръгове се наричат паралели на повърхността на въртене. Минимална обиколкагърло. Максимална обиколка -екватор на повърхност
| Ориз. 33 |
еднакви по форма и размер. Меридианът, лежащ в равнина, успоредна на проекционната равнина, се наричаглавен меридиан.Той формира контура на повърхността. Повърхността на въртене на обща форма също носи едно семейство линии, удобни за конструиране - концентрични окръжности с променлив радиус, разположени в равнината на проекцията, перпендикулярна на оста на въртене.