Регулярни набори и регулярни изрази
Редовни набории регулярни изрази
В този раздел ще разгледаме клас от набори от вериги над краен речник, които са много лесни за описание с формули от някакъв вид. Тези комплекти се наричат редовни.
Дефиниция 1.НекаV1иV2 санабори от низове. Нека дефинираме три операциина тези множества.
Конкатенация (продукт, слепване): Vl V2 = 1, V2> Знакът на операцията за конкатенация обикновено се пропуска.
Нека V n означава произведението на n множества V:V n =VV. V,V° = (тук е празен низ).
3. Итерация: V* = V 0 V 1 V 2 . = =0 ∞ V n .
Дефиниция 4.13.Класът на регулярните множества над краен речникVе дефиниран както следва:

Ако S и T са правилни множества, тогава следните са правилни:
5. Ако едно множество не може да бъде конструирано чрез краен брой приложения на правила 1-4, тогава то е неправилно.
Регулярните множества са добри, защото могат да бъдат описани много просто с формули, които ще наричаме регулярни изрази.
Дефиниция 2.Клас регулярен израз над краен речникVе дефиниран така:

(a V)a е регулярен израз;
Ако R1 и R2 са регулярни изрази, тогава регулярните изрази са:
техният продукт R1R2;
тяхната итерация R1* и R2*.
4. Ако изразът не е конструиран чрез краен брой приложения на правилата 1-3, тогава той не е правилен.
Знакът на продукта може да бъде пропуснат. За да се намали броят на скобите, както във всяка алгебра, се използват приоритетите на операциите: итерацията има най-висок приоритет; по-малко приоритетна работа; добавянето е с най-нисък приоритет.
Примери за регулярни изрази: ab + ba*; (aa)*b+ (с + dab)*.
Очевидно регулярните множества и регулярните изрази са много близки. Но те са различни обекти: регулярният набор е набор от низове (обикновено безкраен), арегулярният израз еформула, която схематично показва как съответният регулярен набор е изграден с помощта на операциите, изброени по-горе(и тази формула е крайна).
Нека R ^ е регулярният набор, съответстващ на регулярния израз R. Тогава:
Ако R =


Ако R = R1+R2, тогава R ^ = Rl^R2 ^ .
Ако R = R1R2, тогава R ^ = R1 ^ R2 ^ .
Ако R = R1*, тогава R ^ = R1^*.
Така регулярният израз е крайна формула, която дефинира безкраен брой вериги, тоест език.
Нека да разгледаме примери за регулярни изрази и съответните им езици.
Всички низове, започващи с b, последвани от произволен брой знаци a
Всички низове от a и b, съдържащи точно две срещания на b
Всички низове от a и b, които съдържат b само по двойки
Всички низове от a и b, съдържащи поне една двойка съседни a или b
Всички низове от 0 и 1, съдържащи подниз 11001
Всички низове от a и b, които започват с a и завършват с b
Очевидно набор от низове е правилен тогава и само ако може да бъде представен чрез регулярен израз. Същият набор от низове обаче може да бъде представен с различни регулярни изрази, например набор от низове, състоящ се от символи a и съдържащ поне две a, може да бъде представен с изрази: aa*a; а*ааа*; ааа*; а*аа*аа* и т.н.
Дефиниция 3.Два регулярни изразаR1иR2се казват, че са еквивалентни(означено сRl = R2)ако и само акоR1^=R2^.
Така aa*a = a*aaa* = aaa* = a*aa*aa*. Възниква въпросът как да се определи еквивалентността на два регулярни израза.
Теорема1.За всякакви регулярни изразиR, SиTвалидно:
R+S = S+R; R+R=R; (R+S)+T = R+(S+T);

R = R = R; (RS)T = R(ST);



R(S+T) = RS+RT; (S+T)R = SR+TR;
R* = +R+R 2 +R 3 + . +R kR*; RR*=R*R; R(SR)* = (RS)*R;
R + \u003d R + R 2 + R 3 +. ; R*R + = RR*; R + + = R*.
Тези отношения могат да бъдат доказани чрез проверка на равенството на съответните набори от вериги. Те могат да се използват за опростяване на регулярни изрази. Например: b (b + aa*b) = b (b + aa*b) = b ( + aa*) b = ba*b. Следователно b (b + aa*b) = ba*b, което не е очевидно.
Регулярните изрази са най-добрите формули, които дефинират регулярните езици. Но крайните автомати имат подобно свойство - те също дефинират езици. Възниква въпросът: как се отнасят един към друг класовете езици, дефинирани от крайни автомати и регулярни изрази? Означете


Теорема2.(Теорема на Клийн.) Класовете на регулярните множества и автоматните езици съвпадат, т.е.


С други думи, всеки автоматен език може да бъде дефиниран чрез формула (регулярен израз) и всеки регулярен набор може да бъде разпознат от краен автомат. Ще докажем тази теорема конструктивно, в две стъпки. На първата стъпка доказваме, че всеки автоматен език е регулярен набор (или, което е същото, за всекикраен автомат, можете да създадете регулярен израз, който указва езика, разпознат от този автомат). На втората стъпка доказваме, че всяко редовно множество е автоматен език (или, което е същото, от всеки регулярен израз можем да конструираме краен автомат, който позволява точно вериги от съответното редовно множество).
Нека въведем модела на графа на прехода като обобщение на модела на крайния автомат. Графът на прехода има един начален и произволен брой крайни върхове, а насочените ребра са маркирани, за разлика от крайния автомат, не със символи, а с регулярни изрази. Графът на прехода допуска верига a, акоaпринадлежи към множеството вериги, описани от произведението на регулярни изрази R1R2. Rn, които маркират пътя от началния връх до един от крайните върхове. Наборът от вериги, позволени от графа на прехода, образува езика, разрешен от него.
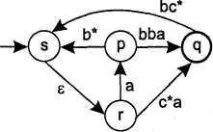
Ориз. 1. Графика на прехода
На фиг. 1 показва графика на прехода, която позволява, например, веригата abbca, тъй като пътят s->r->p->s->r->q, който води до крайното състояние q, е означен с веригата на регулярен израз ab*c*a. Краен автомат е специален случай на преходна графа и следователно всички езици, които са разрешени от автомати, също са разрешени от преходни графи.
Теорема 3.Всеки автоматен език е регулярен набор,


Доказателство. Преходен граф с един начален и един краен връх, чието единствено ребро от началния до крайния връх е обозначено с регулярния израз R, допуска езика R ^ (фиг. 1).
Фиг.2. Графа на преход, допускаща FT на нормален език
Нека сега докажем, че всеки автоматичен език е редовен наборпривеждане на всяка графика на преход без промяна на езика, който позволява, до еквивалентна форма (фиг. 2).
Всеки краен автомат и всеки преходен граф винаги могат да бъдат представени в нормализирана форма, в която има само един начален връх само с изходящи ребра и само един краен връх само с входящи ребра (фиг. 3).
Ориз. 3. Преходен граф с един начален и един краен връх
С преходна графика, представена в нормализирана форма, могат да се извършат две редукционни операции - редуциране на ръбове и редукция на върха - като същевременно се запази езикът, разрешен от тази преходна графика:
а) намаляване на ръба:
б) намаляване на върха (замяната се извършва за всеки път, минаващ през върха p, с последващото му изхвърляне като недостижимо състояние):
Очевидно всяка операция на редукция не променя езика, разпознат от графа на прехода, но намалява или броя на ръбовете, или броя на върховете, и в крайна сметка редукциите ще доведат графа на прехода до формата, показана на фиг. 2. Теоремата е доказана: всеки автоматен език е редовно множество.
Нека е даден краен автомат A:
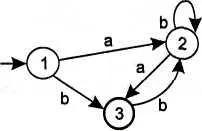
Изграждаме еквивалентна графика на преход в нормализирана форма.
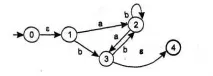
Намаляване на върха 3:
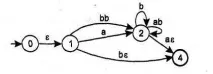
Намаляване на дъгата и прилагане на правилото R = R:
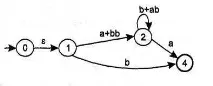
Намаляване на върха 2:
Намаляване на дъга и връх 1:
Така езикът, разпознат от автомат A, е даден от регулярния израз: RA = b+(a+bb)(b+ab)*a.
Нека докажем теоремата на Клийн в другата посока.
Теорема 2.Всеки регулярен набор е автоматен език:


Доказателство.Нека покажем, че за всеки регулярен израз R може да бъде конструиран краен автоматAr (възможно недетерминиран), разпознаващ езика, даден от R. Ще дефинираме такива автомати рекурсивно.
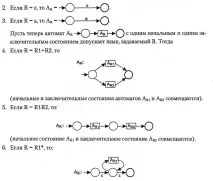
(началното и крайното състояние на A се комбинират).