Решаване на задачи за изчисляване на електрическо съпротивление с помощта на модели
Секции: Физика
Цели:обучение: да се систематизират знанията и способността на учениците да решават проблеми и да изчисляват еквивалентни съпротивления с помощта на модели, рамки и др.
Развитие: развитие на умения за логическо мислене на абстрактно мислене, способност за замяна на схеми за еквивалентност, опростяване на изчислението на схеми.
Образователни: насърчаване на чувство за отговорност, независимост, необходимост от умения, придобити в урока в бъдеще
Оборудване: телена рамка от куб, тетраедър, безкрайна верига от съпротивителни решетки.
1. Учител: "Запомнете последователното свързване на съпротивленията."
Учениците рисуват диаграма на дъската.
Учител: запомнете паралелното свързване на съпротивленията.
Ученикът рисува елементарна диаграма на дъската:
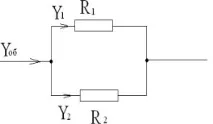
; за за n равно
Учител: И сега ще решим задачи за изчисляване на еквивалентното съпротивление, част от веригата е представена под формата на геометрична фигура или метална мрежа.
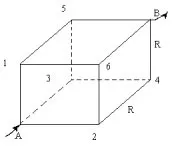
Телена рамка под формата на куб, чиито краища представляват равни съпротивления R. Изчислете еквивалентното съпротивление между точките A и B. За да изчислите еквивалентното съпротивление на тази рамка, е необходимо да смените еквивалентната верига. Точки 1, 2, 3 имат същия потенциал, те могат да бъдат свързани в един възел. И точките (върховете) на куба 4, 5, 6 могат да бъдат свързани с друг възел по същата причина. Учениците имат макет на всяко бюро. След извършване на описаните стъпки се чертае еквивалентна схема.
В AC секцията еквивалентното съпротивление е ; на CD; на БД; и накрая за серийното свързване на съпротивления имаме:
Изчислете RECV. от същия куб, ако кубът е включен във веригата в точки 2 и 4.
По същотопринцип потенциалите на точки А и 6 са равни, В и 3 са равни. Учениците комбинират тези точки на техния модел и получават еквивалентната схема:
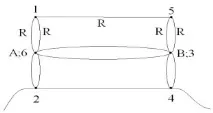
Изчисляването на еквивалентното съпротивление на такава верига е просто.
Същият модел на куб, с включване във веригата между точки 2 и B. Учениците свързват точки с равни потенциали 1 и 3; 6 и 4. Тогава веригата ще изглежда така:
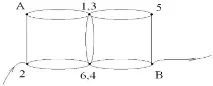
Точки 1.3 и 6.4 имат равни потенциали и токът през съпротивленията между тези точки няма да тече и веригата е опростена до формата; чието еквивалентно съпротивление се изчислява, както следва:
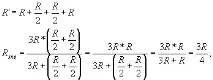
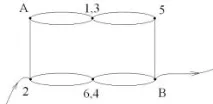
Равностранна триъгълна пирамида, чийто ръб има съпротивление R. Изчислете еквивалентното съпротивление, когато е включено във веригата.
Точки 3 и 4 имат еднакъв потенциал, така че по ръба 3.4 няма да тече ток. Учениците го премахват.
Тогава диаграмата ще изглежда така:
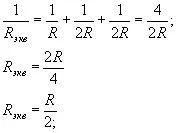
Еквивалентното съпротивление се изчислява, както следва:
Метална мрежа със съпротивление на връзката R. Изчислете еквивалентното съпротивление между точки 1 и 2.
В точка 0 можете да разделите връзките, тогава веригата ще изглежда така:
- съпротивление на едната половина симетрична в 1-2 точки. Успоредно с него е същият клон, следователно
Изчислете еквивалентното съпротивление на телена звезда със съпротивлението на всяка връзка R, включена във веригата между точки 1 и 2.
Звездата се състои от 5 равностранни триъгълника, съпротивлението на всеки.
Между точки 1 и 2 един триъгълник е успореден на четири последователно свързани
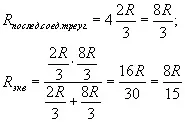
Имайки опит в изчисляването на еквивалентното съпротивление на телени рамки, можете да започнете да изчислявате съпротивлението на верига, съдържаща безкраен брой съпротивления. Например:
Ако разделите връзката
от общата схема, тогава схемата няма да се промени, тогава тя може да бъде представена като
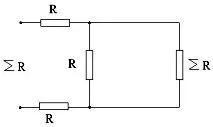
или ,
ние решаваме това уравнение по отношение на Req.
Резултатът от урока: научихме се как да представяме абстрактно части от веригата, да ги заменим с еквивалентни вериги, които улесняват изчисляването на еквивалентното съпротивление.
Изчислете еквивалентното съпротивление на телената рамка от две окръжности с радиуси r1 и r2, r2=2r1 между точките A и B. Единична дължина на съпротивлението на проводника?
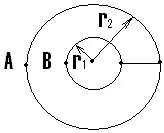
Забележка: Този модел трябва да бъде представен като: