Шпори на хидро

17. Режим на турбулентен поток. Основен поток св-ва. Структура на потока

турбулентният поток се характеризира със смесване на флуиди, колебания на скоростта и налягането. Ако с помощта на особено чувствителен рекордер измерваме и записваме пулсации, например скорости във времето във фиксирана точка на потока, тогава ще получим картина, подобна на тази, показана на фиг. 1.54. Скоростта се колебае произволно около някаква средна стойност y0av n0, времевата стойност, която в този случай остава постоянна!

Траекториите на частиците, преминаващи през дадена фиксирана точка в пространството в различни моменти от време, са извити линии с различни форми, въпреки правотата на тръбата. Характерът на линиите на тока в тръбата в даден момент също е много разнообразен (фиг. 1.55). Така^

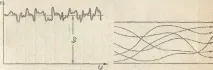
Rns. 1.54. Пулсиране на скоростта в обиколка - Фиг. 1.55. Характер на линиите на потока в бурентния поток турбулентен поток

Строго погледнато, турбулентният поток винаги е нестабилен, тъй като стойностите на скоростите и наляганията, както и траекториите на частиците, се променят с времето. Въпреки това, той може да се счита за постоянен поток, при условие че осреднените във времето стойности на скоростите и наляганията, както и общият дебит не се променят с времето. Такъв курс се среща доста често в практиката.

18. Особености на турбулентното движение на течността. Пулсиране на скорости и налягания. Напрежение на срязване при турбулентен поток.

Разпределението на скоростите в турбулентния поток е по-равномерно и увеличаването на скоростта в близост до стената е по-стръмно, отколкото в ламинарен поток, който се характеризира с параболичен закон на разпределение на скоростта.

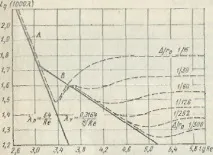
Поради товакоефициентът на Кориолис a, който отчита неравномерното разпределение на скоростите в уравнението на Бернули, е много по-малък при турбулентен поток, отколкото при ламинарен поток. За разлика от ламинарния поток, къдетоане зависи от Re и е равно на 2, тук коефициентътае функция на Re и намалява с нарастването на последното от 1,13 при Re ==Recr до 1,025 при Re = 3-10 6 . Както се вижда от графиката,

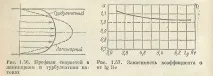
показано на фиг. 1.57 *, криватаaсе доближава до единица с увеличаване на числото Ke, следователно в повечето случаи при турбулентен поток може да се приемеa= 1.

Тъй като при турбулентния поток няма наслояване на потока и се получава смесване на течности, законът на триене на Нютон в този случай изразява само малка част от общото напрежение на срязване. Поради смесването на течността и непрекъснатото предаване на инерция в напречна посока, напрежението на срязване t0 върху стената на тръбата при турбулентен поток е много по-голямо, отколкото при ламинарен поток, при същите стойности на числото Re и динамичното налягане

V 2 /2, изчислено от средната скорост на потока.

19. Загуби на енергия от триене по дължината на турбулентен поток в кръгъл тръбопровод.

Ако при ламинарен поток загубата на налягане поради триене се увеличава пропорционално на скоростта (дебита) до първа степен, тогава при прехода към турбулентен поток се забелязва известен скок в съпротивлението и след това по-рязко увеличение на стойността на htr по крива, близка до парабола от втора степен.

Поради сложността на турбулентния поток и трудностите при аналитичното му изследване, до момента няма достатъчно строга и точна теория за него. Има полуемпирични, приблизителни теории, като теорията на Praidtl** и други, които не са включени тук.са считани.

* За първи път получен от Б. Б. Некрасов

В повечето случаи за практически изчисления, свързани с турбулентния поток на течности в тръбите, се използват експериментални данни, систематизирани въз основа на теорията за хидродинамичното подобие.

Основната формула за изчисляване на загубите на напор при турбулентен поток в кръгли тръби е емпиричната формула, вече дадена по-горе като емпирична формула, наречена формула на Вайсбах-Дарси и имаща следната форма

Тази основна формула е приложима както за турбулентен, така и за ламинарен поток, разликата се състои само в стойностите на коефициента

,.Тъй като при турбулентния поток загубата на налягане поради триене е приблизително пропорционална на скоростта (и потока) на втора степен, коефициентът на загуба на триене във формулата в първото приближение за дадена тръба може да се счита за постоянна стойност.

20. Коефициент на хидравлично триене в турбулентен поток. Концепцията за грапавостта и нейното влияние върху

.

От закона за хидродинамичното подобие обаче следва, че коефициентът

, както иl,, трябва да бъдат функция на основния критерий за подобие на потоците под налягане - числото на Рейнолдс Re, и може също да зависи от безразмерния геометричен фактор - относителната грапавост на вътрешната повърхност на тръбата, т.е.=f(Re,/d), къдетое средната височина на заоблеността на туберкулите, d,— диаметър на тръбата.

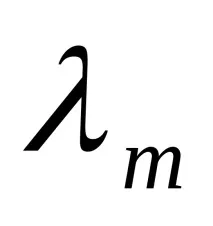
Когато грапавостта на тръбата не влияе на нейната устойчивост (с

t), тръбата се нарича хидравлично гладка. За тези случаи коефициентът Rt е функция само на числото на Рейнолдс:m=f1(Re). Съществуват редица емпирични и полуемпирични формули, изразяващи тази функция за турбулентен поток в хидравлично гладки тръби; единот най-удобните и често срещани е формулата на П. К. Конаков

приложимо, когато броят на Re от Rekr до Re е равен на няколко милиона.

При 2300 8 можете също да използвате формулата на Blasius

21. Графики от Nmkuradze

I. I. Nikuradze тества серия от тръби с изкуствено създадена грапавост на вътрешната им повърхност за устойчивост. Грапавостта се получавала чрез слепване на пясъчни зърна с определен размер, получени чрез пресяване на пясък през специални сита. Така се получава равномерно разпределена гранулирана грапавост.

П

Първата област е областта на малки Re и/r0, където коефициентътm не зависи от грапавостта, а се определя само от числото Re; това е областта на хидравлично гладките тръби. Няма място за максималните стойности на грапавостта в експериментите на И. И. Никурадзе.

Във втората област коефициентът

m зависи едновременно от два параметъра - числото Re и относителната грапавост.

Третата област е областта с големи Re и

/r0, където коефициентътm не зависи от Re, а се определя само от относителната грапавост. Тази област се нарича самоподобна област или режим на квадратично съпротивление, тъй като независимостта на коефициентаmот Be означава, че загубата на напор е пропорционална на скоростта на втора степен

За да се разберат по-добре тези характеристики на съпротивлението на грубите тръби, е необходимо да се вземе предвид наличието на ламинарен слой.

Както бе споменато по-горе, с увеличаване на Be, дебелината на ламинарния слой

l намалява, следователно, за турбулентен поток при малък Re, дебелината на ламинарния слой е по-голяма от височината на неравностите, последните са разположени вътре в ламинарния слой, текат плавно (без отделяне) и не влияят на съпротивлението. С увеличаването на Re дебелинатаlнамалява, неравностите започват да излизат извън слоя и да влияят на устойчивостта. При големи Re дебелината на ламинарния слой става много малка и туберкулите на грапавостта се движат в турбулентен поток с вихрови образувания зад всеки туберкул; това обяснява квадратичния закон на съпротивлението, характерен за този регион.

Графиката на I. I. Nikuradze ви позволява да изградите приблизителна зависимост от Be на допустимата грапавост, т.е. такава максимална стойност, при която грапавостта на тръбата все още не влияе на нейната устойчивост. За да направите това, вземете тези точки на графиката (вижте фиг.), в които кривите за грапави тръби започват да се отклоняват от правата линияBза гладки тръби. Очевидно с увеличаване на Re стойността на допустимата грапавост намалява.

22. Основните видове локална резистентност. Коефициент на местни загуби

Най-простите местни хидравлични съпротивления могат да бъдат разделени на разширения, стеснения и завои на канала, всеки от които може да бъде внезапен или постепенен. По-сложните случаи на локални съпротивления са съединения или комбинации от изброените най-прости съпротивления. Така например, когато течност тече през клапан, потокът се огъва, променя посоката си, стеснява се и накрая се разширява до първоначалните си размери; в този случай се получава интензивно образуване на вихри.

Нека разгледаме най-простите локални съпротивления в режим на турбулентен поток в тръба. Коефициентите на загуба

,в турбулентния поток се определят главно от формата на местните съпротивления и се променят много малко с промените в абсолютните размери на канала, скоростта на потока и вискозитетана течността, т.е. с промяна в числото Re, поради което обикновено се приема, че те не зависят от Re, което означава квадратичен законсъпротива или самоподобие.

---