Силов момент около оста, Платформа за съдържание

Въртящ момент на ос
Проекционната лема ни позволява да въведем нова характеристика на силата по отношение на оста. Определение.Моментът на силата F спрямо оста zе алгебрична стойност, равна на проекцията на момента на силата върху тази ос спрямо произволна точка от определената ос.
mz(F)=przmA(F)(A принадлежи на z) (17)
Помислете за метода на изчисление и свойствата на момента. Използвайки произвола на избора на центъра на моментите върху оста, ние избираме като такъв m.O - проекцията на точката A на прилагане на силата върху оста z. Означавайки сkединичния вектор на z-оста и прилагайки кръгова пермутация в смесения продукт, пишем
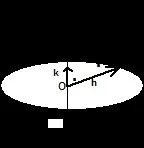
Тук се има предвид, че поради взаимната перпендикулярност на векторитеkиOA,, модулът на произведениетоkxOAе равен на разстоянието OA от точката на прилагане на силите спрямо оста.
Формулата показва, че:
а) Моментът около оста се дава само от компонента на силата, насочена по допирателната t към окръжността с радиус h.
б) Знакът на момента се определя от знака Коза. От фиг.8 следва
Фиг.8 следното правило на знаците:Моментът на силата около оста е положителен, ако се вижда от края на оста, че силата се стреми да завърти тялото обратно на часовниковата стрелка.
От формула (12) следва, че моментът на силата спрямо оста е равен на нула, ако силата и оста лежат в една и съща равнина (a=p/2). Случва се, когато
1) силата е успоредна на оста
2) линията на действие на силата пресича оста
Алгебричен момент на сила спрямо центъра за плоска система от сили.
Системата от сили, разположени в една равнина, се наричаплоска. Нека поставим оста xy в равнината на действие на силите с начало в произволна точка О на равнината. В този случай силитесъздават момент само около оста z, перпендикулярна на равнината на действие на силите. Поставяйки силите върху равнината на листа, читателят вижда оста като точка O и нарича момента спрямо тази осалгебричния момент на сила спрямо точкатаO
Правило на знаците: Моментът е положителен, ако се вижда, че силата се стреми да обърне тялото срещу
Основният момент на системата от сили. Зависимост на главния момент от центъра.
Определение:Основният моментна системата от сили спрямо центъра O е векторната сума на моментите на всички сили на системата спрямо този център.
На практика основният момент се установява чрез неговите проекции върху декартовите оси. Логично е да наречем тези проекции основните моменти на системата от сили спрямо осите x, y, z.
MA2=Mx2+My2+Mz2; Mx=Smx(Fk); My=Smy(Fk); Mz=Smz(Fk)
Нека намерим връзката между основните моменти по отношение на два центъра A и B. Обобщавайки предварително получената зависимост за една сила върху всички сили на системата, получаваме:
Тук се взема предвид определението на главния вектор V.
Ротационна система. Двойка правомощия.
Формула (4) показва, че в общия случай основният момент зависи от центъра.
Ако обаче главният вектор на системата е равен на нула, тогава нейният главен момент не зависи от центъра. Нека наречем такава система от силиротационна система.
Най-простата ротационна система едвойкасили: система от две противоположно насочени сили, равни по абсолютна стойност, които не лежат на една права линия.
Разстоянието h между линиите на действие на силите на двойката се нарича рамо на двойката.
Главният вектор на силата на двойката очевидно е равен на нула, така че неговият главен момент не зависи от центъра, нарича семомент на двойкатаmи може да се намери като момент на една от силите на двойката около точкатаприложения на втората сила.
Моментът на двойката е перпендикулярен на равнината на двойката и насочен настрани,
откъдето може да се види, че двойката има тенденция да върти тялото обратно на часовниковата стрелка.
Условия на покой за дискретна механична система.
Механичната система се състои от материални точки. Тя ще бъде в покой, ако всяка от точките на системата е в покой. Следователно е логично първо да се изследват условията на покой на материална точка. Те следват от принципите на механиката.
Принципи (аксиоми) на механиката. Точкови условия на почивка.
Както всички точни науки, механиката се основава на недоказуеми постулати, произтичащи от опита и наречени аксиоми. Плод на мисленето на много поколения изследователи, аксиомите са окончателно формулирани от Исак Нютон през 17 век и затова носят неговото име.
1.Галилеевият принцип на инерцията
Има референтна система, наречена инерционна, в която изолирана точка остава в покой.
Изолирана точка е точка, която не взаимодейства с други точки.
Така точката остава в покой, докато върху нея не действа сила. Трябва да се отбележи, че отправната система, свързана със Земята, не е инерционна поради въртенето на Земята.
2.Основен принцип (втори закон на Нютон)
Ускорението на материална точка е пропорционално на силата, действаща върху нея.
Принципът показва, че резултатът от действието на сила е промяна в скоростта (състоянието) на дадена точка и това действие е толкова по-малко, колкото по-голяма е масата на тялото. В бъдеще всички сили ще се сравняват с ускоренията, които предизвикват. Силите, причиняващи равни ускорения, се наричат резултантни или еквивалентни.
3.Принцип на равенство на действието и реакцията(третият закон на Нютон). Свойства на вътрешните сили.
Силите на взаимодействие на две точки са равни по големина, противоположни по посока и лежат на права линия, минаваща през точките.
Трябва да се отбележи, че тези сили се прилагат към различни точки и следователно в общия случай те не се балансират взаимно. Ако точките принадлежат на едно и също тяло, тогава силите на тяхното взаимодействие се наричат вътрешни (индексi). Тъй като всички вътрешни сили са сдвоени, очевидно е, че главният им вектор (сума) и главният момент са равни на нула.
4.Принцип на независимо действие на силите
Досега въпросът за смисъла и приложимостта на вятърните операции към силите остава открит. Следният принцип позволява добавянето на сили в точка в смисъл, че добавянето не променя ускорението на точката.
Ускорението на точка под действието на система от сили е равно на векторната сума на ускоренията на точка от всяка сила на системата поотделно.
а) Силите, приложени към точка, имат резултат, равен на векторната сума на началните сили (правило на паралелограма). Всъщност, според втората аксиома:
Вторият закон на Нютон вече може да бъде написан и за случая на действие на няколко сили.
б) В покой остава не само изолирана точка, но и точка под действието на сили, чиято сума е нула. По този начин,необходимо и достатъчно условие за баланса на силите, приложени към точкатае
Условия на покой за произволна дискретна механична система
Да разгледаме дискретна система от n материални точки. Една система е в покой, ако всички нейни точки са в покой. В този случай силите, действащи върху всяка точка, са в равновесие.
Нека означим с Fke равнодействащата на външните сили, приложени към точката с номер k, а с Fki равностойната на вътрешните сили на тази точка.От аксиомите следва, че условията
Fke+ Fki=0 (k=1,2,…,n), (12)
осигуряват останалата част от системата и санеобходими и достатъчни условияза баланса на силите, приложени към произволна дискретна механична система.
Необходими условия за равновесие на външните сили на системата.
Ако системата е в покой, тогава всяка комбинация или част от условията (12) е изпълнена и следователно е необходимо, но не достатъчно условие за равновесие.
Вътрешните сили на системата обикновено са неизвестни, така че комбинацията от условия (12), която изключва тези сили, е от особен интерес. Свойствата на сдвояване на вътрешните сили позволяват да се правят такива комбинации.
Сумирайки (12) по k и като вземем предвид, че главният вектор на вътрешните сили е равен на нула, получаваме
Векторно умножавайки (12) отляво по радиус вектора на точката rk, след сумиране получаваме второто условие
И двете условия засягат само външните сили на системата и санеобходими, но не и достатъчниусловия на покой запроизволна механичнасистема. По-нататък ще покажем, че те са необходими и достатъчни условия за покой на твърдо тяло.