Svertochnye_kody - Страница 4
Важна характеристика на кода, която напълно определя неговите коригиращи свойства, е спектърът на свободните разстояния на кода, т.е. изброяването на броя кодови последователности, които имат дадена стойност на свободното разстояние [15, 23].
Минималното свободно разстояние d L на конволюционен код може да се определи с помощта на диаграма на състоянието или решетъчна диаграма за съответния енкодер.
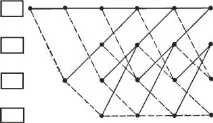
Тъй като конволюционният код е линеен код, сред различните пътища на решетъчната диаграма на кода задължително ще има път с нулево тегло (нулев път), т.е. път, чиято последователност от кодови символи се състои изцяло от нули. Следователно минималното свободно разстояние на конволюционния код ще бъде равно на минималния брой единици, т.е. минималното тегло на пътищата, които се разминават и се сливат с нулевия път. Диаграмата на кодовата решетка може да се използва за определяне на минималното свободно разстояние, ако за всеки от нейните клонове се запише теглото на съответните кодови символи на изхода на енкодера и след това се изчисли теглото на пътищата, които се разминават и сливат с нулевия път. На фиг. Фигура 5.1 показва подобна решетъчна диаграма с тегловни етикети за конволюционен енкодер (фиг. 2.5b), изграден на базата на решетъчната диаграма (фиг. 4.2).
Ориз. 5.1. Решетъчна диаграма с тегловни етикети за енкодера (фиг. 2.5, b)
От него се вижда, че от всички ненулеви пътища, които се разминават и сливат с хоризонталния нулев път, ще има един с тегло 5, отклоняващ се от нулевия път с 3 клона
два пътя, отклоняващи се от нулевия път с 4
и 5 клона и с тегло w = 6
По този начин минималното тегло на ненулев път за даден конволюционен код е 5, следователноминималното свободно разстояние на този код е d min = 5. Очевидно този код може да коригира (вижте параграф 11 по-долу) всякакви две грешки, възникнали в комуникационния канал, тъй като тези две грешки могат да доведат до факта, че получената последователност от кодови символи ще има разстояние на Хемминг от предадената последователност, равно на две, а от всички други последователности това разстояние ще бъде поне не по-малко от три. Следователно, когато се декодира с минимално разстояние на Хемминг, всеки две грешки ще бъдат коригирани от този код.
Очевидно е, че потенциалната коригираща способност на конволюционния код е толкова по-висока, колкото по-голямо е неговото минимално свободно разстояние. Следователно, структурата на енкодера на конволюционния код, т.е. неговите генериращи полиноми, се стреми да бъде избрана по такъв начин, че да максимизира минималното свободно разстояние на кода. Това, при други равни условия, осигурява най-високата коригираща способност на конволюционния код при декодирането му до максимална вероятност, по-специално при декодиране с помощта на алгоритъма на Viterbi (вижте раздел 8.3).
Наред с оценката на минималното свободно разстояние на конволюционния код от решетъчната диаграма, стойността d min може да се определи от последователността на изходните символи B(X) – по цялата дължина на кодовото ограничение l П (5.7).
В табл. 5.1, въз основа на конструкцията на B(X) на интервала l P, последната колона показва стойностите d min на съответните кодове, които са равни на теглото w на последователности B(X):
където W l P е теглото на кодовата последователност върху пълната дължина на кодовото ограничение l P .
Обърнете внимание, че за енкодера на фиг. 2.5, b (втори ред на таблица 5.1) изходната последователност B(x) в структурата напълно съвпада със структурата на изходния код, когато последователността A(X) = влезе във входа на енкодера1000… за диаграмата на решетка (фиг. 4.2), тъй като пътят по решетка определя идентичността B(X) = 111011000….
По този начин минималното свободно разстояние d min за различни варианти на къси конволюционни кодове може да бъде намерено чрез (5.14) чрез определяне на структурата на изходната последователност B(X) на дължината l P (Таблица 5.1.), което се прави при извършване на лабораторна работа.
11. Коригиращата способност на кода се определя от множествеността (броя) на коригираните g И грешки, което се разбира като гарантиран брой грешки в кодови комбинации, коригирани от даден код. Очевидно, колкото по-голяма е множествеността на g И, толкова по-ефективен е кодът. Хеминг идентифицира проста връзка между стойността на минималното кодово разстояние и гънката на грешката. Получената кодова последователност, засегната от смущения, се идентифицира от приемащата страна с тази от информацията, с която е най-сходна, т.е. с тази, от която се различава с по-малък брой символи. Хеминг показа, че това е вярно за блоковите кодове при условието
откъдето следва, че
x означава цялата част от числото x.
При конволюционното кодиране множеството коригираеми грешки се определя от подобен израз, като се взема предвид минималното свободно разстояние d L при обработка на кодови последователности с дължина L. Ако в последователността са възникнали не повече от g И грешки, при-
от g и удовлетворява неравенството
тогава грешките се коригират.
По-специално, когато дължината L на кодовата последователност е равна на общата дължина на кодовото ограничение l P , в съответствие с (5.11),
което съвпада с (5.15) и (5.16) за блокови кодове, тъй като постоянната дължина на блоковия код е еквивалентна на пълната дължина на кодовото ограничение за конволюционните кодове.
12. Силата на кода определяспособността на кодовете да коригират множество, единични и множество грешки, които възникват в канала
le връзка. Силата на кода зависи от входната дължина на кодовото ограничение l (5.5) и от формата на генериращите полиноми. В [23] беше показано, че вероятността за коригиране на грешки по време на декодиране е изрично свързана със свободното кодово разстояние d L . И така, за разгледания по-рано енкодер (фиг. 2.5, b), който генерира кода (2, 1, 3) с генериране на поли-
номинали G 1 и G 2 (Таблица 5.1), стойността d min = 5. За кода (2, 1, 5) с генериращи полиноми
G 1 (X) \u003d 1 + X 3 + X 4,
който се използва при кодиране на говорен сигнал в клетъчната комуникационна система GSM, d min = 7. В още по-мощен код (2, 1, 7) с генериране на полиноми
G 1 (X) \u003d 1 + X 2 + X 3 + X 5 + X 6,
(X) = 1 + X + X 2 + X 3 + X 6,
използвани в сателитни комуникационни системи, d min = 10. Следователно кодовете с голямо кодово ограничение l са
13. Енергийното усилване на кода η определя усилването на шумоустойчивостта при прилагане на коригиращо кодиране. Като правило системите предполагат използването на символи с фазова модулация за включване и изключване, използвайки противоположни сигнали с начална фаза 0 ° при предаване на символ „1” и 180 ° при предаване на „0” (или обратно).
За да се получи дадена стойност на вероятността за погрешно приемане на един символ p 1 в информационната последователност, е необходимо да се осигури на изхода на демодулатора на приемника някакво необходимо минимално допустимо съотношение сигнал / шум.
При предаване на информация с коригиращо кодиране, вместо k информационни символа за дадено време, се изисква предаване на n символа с добавяне на тестови символи за същото време при същото ниво на сигнала.
Това ще намали продължителносттасимволи по време на предаване (при скорост R = 1/3 - три пъти), което ще изисква разширяване на честотната лента с n/k пъти. Първоначалната зададена стойност на вероятността p 1 вече ще бъде осигурена с различно съотношение сигнал/шум. Разликата в съотношенията сигнал/шум със и без кодиране на неговата позиция
жизнената стойност определя енергийната печалба на кода, изразена в децибели.
Прави се бърза приблизителна оценка на енергийната ефективност за целите на оперативното сравнение на кодове по асимптотиката
mu енергия печалба от кодиране (AEEC)
η = 10lgRd min (dB),
където R = k/n е относителната кодова скорост; d min е минималното кодово разстояние.
Стойността на AEEC характеризира EVK при вероятност p 1 → 0 и е горната граница на реалния EVK при p 1 ≠ 0 [23].
В табл. 5.2 показва основните характеристики на къси конволюционни кодове със скорост R = 1/2, показващи стойностите на AEEC.
Кодовете са дадени чрез генериране на полиноми в осмична нотация и са посочени стойностите на кодовата памет (5.5) и минималното кодово разстояние (5.11).
Печалбата от кодирането може да се използва по най-ефективния начин, например чрез намаляване на мощността на предавателите в комуникационните системи, чрез намаляване на размера на антените или чрез увеличаване на скоростта на предаване.
Както е отбелязано в [15], конволюционните кодове с малка дължина на ограничението на кода и декодирането с помощта на алгоритъма на Viterbi са най-подходящи за получаване на значителна печалба от кодирането. По-специално, добре познатият код с R = 1/2, l = 6, който има GEC от 5 dB при p 1 = се използва в много системи при различни скорости на предаване на данни.
14. Сложността на конволюционните кодеци определя възможността за практическо прилагане на енкодера от страната на предаване и декодераот приемащата страна на комуникационната система.
Сложността на конволюционния енкодер се определя от броя на неговите най-прости елементи, които са битове в регистъра за изместване, суматори по модул 2 и връзки на суматори с битове за изместване. В повечето случаи дължината на преместващия регистър е от порядъка на няколко десетки единици и всеки суматор е свързан с приблизително половината от битовете на регистъра. Следователно можем да предположим, че сложността на конволюционния енкодер зависи линейно от дължината на регистъра m или от дължината на кодовото ограничение l. Практическото изпълнение на устройство, състоящо се от няколко десетки или стотици прости елементи, не е трудно.
Сложността на декодерите се определя от метода на декодиране. В момента се използват три основни метода за декодиране на конволюционни кодове: прагов, подобен на основния метод за декодиране на блокови кодове, последователен и декодиране с помощта на алгоритъма на Viterbi.
Най-лесните за изпълнение са алгоритмите за декодиране на мнозинството както за блокови, така и за конволюционни кодове. Сложността на внедряването на декодери расте почти пропорционално на общата дължина на кодовото ограничение l П (5.7). Декодерите са доста прости при коригиране на грешки с ниска множественост (g I = 1, 2). Въпреки това, по-нататъшното увеличаване на множеството коригиращи грешки води до значително усложняване на конструкцията на веригата на декодери, което не е оправдано от увеличаване на стойността на EEC.
Декодерите на Viterbi имат най-голяма сложност, чието количество изчисления (сложност) нараства експоненциално с дължината на кодовото ограничение. При използване на алгоритъма на Viterbi, увеличаването на DCO с един повече от два пъти обема на декодера, но дава увеличение на GEC - 0,4 ... 0,5 dB [23]. Следователно практически използваните декодери се изпълняват за кодове с DCO l ≤ 7…8. ПовишетеСкоростта на такива декодери е възможна чрез паралелизиране на процедурите за декодиране и намаляване на обема - поради прехода към микропроцесорна технология.
15. Надеждност на кодирането - определя се от вероятността за правилно декодиране на предаваната информационна последователност. Очевидно не всеки избор на връзки в конволюционния енкодер ще доведе до добра конструкция на енкодера. Например, очевидно е лошо да се свързва всеки от суматорите с едни и същи битове на регистъра.
До голяма степен надеждността на кодирането се определя от набора от кодови разстояния между последователностите, генерирани от енкодера.
За да изградите добър конволюционен код, трябва да намерите дефиниращи кодове, които генерират полиноми или матрици, които определят връзките между суматорите и регистриращите кранове. Конструкцията се извършва въз основа на получаване на максималната EEC или минималната DTC l за даден d min , или минималната вероятност за повреда на символа. Търсенето на кодове се извършва, като правило, чрез изброяване на компютър. Към днешна дата са открити голям брой конволюционни кодове с различни параметри за борба с различни видове смущения.
16. Трудоемкост - характеризира процеса на декодиране на конволюционен код и се определя от броя на изчислителните операции, изразходвани за декодиране на един съответен блок от получената последователност от знаци. Ясно е, че ако необходимият брой операции за единица време за всеки метод за декодиране на даден конволюционен код надвишава скоростта на съществуващата компютърна технология, тогава такъв код не представлява практически интерес. В този случай ще бъде необходимо по-специално да се намали техническата скорост на предаване.
След като разгледахме редица параметри и характеристики на конволюционните кодове, нека преминем към кратък преглед на разновидностите на тези кодове.
6.РАЗНООБРАЗИЕ ОТ КОНВОЛЮЦИОННИ КОДОВЕ
6.1. Систематични и несистематични кодове
Ако в последователността от кодови символи, генерирани от енкодера, е възможно да се отделят r = n - k излишни символа от k информационни, тогава кодът се нарича систематичен. В систематичен енкодер ще има информационни последователности на k изхода. На другите изходи има поредици от символи за проверка, формирани като линейни комбинации от информация.
Първите k изхода на систематичния енкодер са свързани директно към първите битове на регистрите. Кодовете на Fink са систематични; на фиг. 2.5 показва: а) - систематични, б) - несистематични енкодери с кодова скорост R = 1/2, т.е. с k = 1. За енкодери с k = 1, при генериране на систематични кодове, един от генериращите полиноми е или G 1 (X) = 1, или G 2 (X) = 1, така че информационната последователност е част от изходната последователност.
Систематичните кодове позволяват да се получи оценка на информационните символи от приемащата страна без декодиране или друга обработка на получените символи. Информацията не се съдържа директно в несистематични кодови последователности; те трябва да бъдат конструирани по такъв начин, че при липса на грешки да могат лесно да бъдат възстановени в декодера.
Предимството на несистематичните конволюционни кодове е, че тяхното минимално свободно разстояние е по-голямо от това на систематичните, при равни други условия.
Това се дължи на факта, че системата
Един систематичен математически конволюционен код може