Свойства и методи за намиране на корените на квадратно уравнение

Светът е устроен по такъв начин, че решаването на голям брой проблеми се свежда до намирането на корените на квадратно уравнение. Корените на уравненията са важни за описване на различни модели. Това е било известно дори на геодезистите на древен Вавилон. Астрономите и инженерите също бяха принудени да решават подобни проблеми. Още през 6-ти век след Христа индийският учен Арябхата разработи основите за намиране на корените на квадратно уравнение. Формулите придобиват завършен вид през 19 век.

Общи понятия

Предлагаме ви да се запознаете с основните закони на квадратните равенства. Най-общо равенството може да се запише по следния начин:

Броят на корените на квадратното уравнение може да бъде равен на един или два. Бърз анализ може да се направи с помощта на концепцията за дискриминант:

В зависимост от изчислената стойност получаваме:

Когато D > 0 има два различни корена. Общата формула за определяне на корените на квадратно уравнение изглежда като (-b± √D) / (2a).
D = 0, в този случай коренът е единица и съответства на стойността x = -b / (2a)
D2 + bx = -c

Умножаваме дясната и лявата част по 4a и добавяме b 2, получаваме

4a 2 x 2 + 4abx + b 2 = -4ac+b 2

Нека трансформираме лявата страна като квадрат на многочлена (2ax + b) 2 . Извличаме квадратния корен от двете части на уравнението 2ax + b = -b ± √ (-4ac + b 2 ), прехвърляме коефициента b от дясната страна, получаваме:

2ax \u003d -b ± √ (-4ac + b 2 )

Което трябваше да се покаже.

специален случай

В някои случаи решението на проблема може да бъде опростено. И така, за четен коефициент b получаваме по-проста формула.

Означаваме k = 1/2b, тогава формулата на общата форма на корените на квадратното уравнение приема формата:

x \u003d (-k ± √ (k 2 - ac)) / a

За D = 0 получаваме x = -k / a

другичастен случай е решението на уравнението за a = 1.

За формата x 2 + bx + c \u003d 0, корените ще бъдат x \u003d -k ± √ (k 2 - c) с дискриминант по-голям от 0. За случая, когато D \u003d 0, коренът ще бъде определен по проста формула: x \u003d -k.

Използване на графики

Забележка: Крива, построена на базата на квадратична функция, се нарича парабола.

Нека дадем няколко примера.

При изчисляване на траекторията на снаряд се използва свойството на движение по парабола на тяло, изстреляно под ъгъл спрямо хоризонта.
Свойството на параболата да разпределя равномерно натоварването се използва широко в архитектурата.

Разбирайки важността на параболичната функция, нека разберем как да използваме графиката, за да изследваме нейните свойства, като използваме понятията "дискриминант" и "корени на квадратно уравнение".

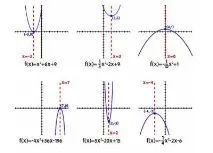
В зависимост от стойността на коефициентите a и b има само шест опции за позицията на кривата:

Дискриминантът е положителен, a и b имат различни знаци. Клоновете на параболата гледат нагоре, квадратното уравнение има две решения.
Дискриминантът и коефициентът b са равни на нула, коефициентът a е по-голям от нула. Графиката се намира в положителната зона, уравнението има 1 корен.
Дискриминантът и всички коефициенти са положителни. Квадратното уравнение няма решение.
Дискриминантът и коефициентът a са отрицателни, b е по-голямо от нула. Клоните на графиката са насочени надолу, уравнението има два корена.
Дискриминантът и коефициентът b са равни на нула, коефициентът a е отрицателен. Параболата гледа надолу, уравнението има един корен.
Стойностите на дискриминанта и всички коефициенти са отрицателни. Няма решения, стойностите на функцията са изцяло в отрицателната зона.

Забележка: опцията a = 0 не се взема предвид, тъй като в този случай параболатаизражда в права линия.

Всичко по-горе е добре илюстрирано на фигурата по-долу.

Примери за решаване на проблеми

Условие: използвайки общи свойства, съставете квадратно уравнение, чиито корени са равни един на друг.

по условието на задачата x1 = x2, или -b + √(b 2 - 4ac) / (2a) = -b + √(b 2 - 4ac) / (2a). Опростяване на въвеждането:

-b + √(b 2 - 4ac) / (2a) - (-b - √(b 2 - 4ac) / (2a)) = 0, отворете скобите и дайте подобни членове. Уравнението приема формата 2√(b 2 - 4ac) = 0. Това твърдение е вярно, когато b 2 - 4ac = 0, следователно b 2 = 4ac, тогава стойността b = 2√(ac) се замества в уравнението

ax 2 + 2√(ac)x + c = 0, в намалената форма получаваме x 2 + 2√(c / a)x + c = 0.

за a, което не е равно на 0 и всяко c, има само едно решение, ако b = 2√(c / a).

Квадратните уравнения, въпреки цялата им простота, са от голямо значение в инженерните изчисления. Почти всеки физически процес може да бъде описан с известно приближение, като се използват степенни функции от порядък n. Квадратното уравнение ще бъде първото такова приближение.