Свойства на ентропийната функция на източника на дискретни съобщения
Свойствата на ентропийната функция могат да бъдат ясно демонстрирани с помощта на примера на източник на дискретни съобщенияA=(a1, a2) с размер на азбукатаmравен на 2, т.е.m=2. В този случай , и изразът (1.8) може да се запише като:
(бит/символ).
Графиката на тази функция има формата, показана на фиг. 1.1.
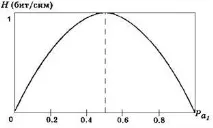
Фиг.1.1. Графика на ентропийната функция.
От графиката се вижда, че превръщането на вероятността за поява на един от възможните символи на 0 или 1 въвежда пълна сигурност, ентропията се превръща в 0, а съобщението за приемането на такъв знак не съдържа никаква информация.
Когато се получи определен символ, той е най-несигурен и количеството информация, съдържащо се във входящия символ, е максимално.
Анализът на формула (1.8) и графика (фиг. 1.1) ни позволява да формулираме основните свойства на ентропийната функция.
1 Ентропията на източника на дискретни съобщения е реална, ограничена и положителна величина.
2 Ентропията е 0, ако винаги се избира един и същ символ с вероятност единица.
3 Ентропията е максимална, ако всички символи на източника на съобщение се появяват независимо и с еднаква вероятност.
Интересно е да се отбележи, че сравнението на изрази (1.5), (1.7) и (1.10) показва, че формулата на Хартли е специален случай на формулата на Шанън при условие, че в съобщението се появяват символи, а формулата на Шанън, от своя страна, е специален случай на условна ентропия, при условие че символите на съобщението са независими. Действително, от (1.10) следва, че количеството информация, съдържащо се в съобщение, състоящо се отnнееквивероятни взаимно зависими символа, се определя от израза:
.
Ако символите на съобщението са взаимно независими, тогава и ,следователно този израз се преобразува във формата:
=
Последният израз съответства на формулата на Шанън.
В случай на равновероятно появяване на символи за съобщения, заj=1, 2,…,m.(m– обемът на азбуката) и горният израз за формулата на Шанън след съответното преобразуване ще приеме формата:
,
което отговаря на формулата на Хартли.
Така определеното от Хартли количество информация, т.е. приемайки пълна независимост и еднаква вероятност за поява на отделни знаци от съобщението, определя максимално възможното количество информация в съобщение с дадена дължина (n).
При неравна вероятност за поява на знаци (формула на Шанън), количеството информация, съдържащо се в съобщение с дадена дължина (n), се намалява. Друг фактор, който намалява ентропията и, следователно, количеството информация в съобщение с дадена дължина (n), е наличието на статистическа зависимост между символите - корелации.
Поради корелациите между символите и тяхната неравномерна поява, количеството информация в реалните съобщения намалява. Количествено, тези загуби на информация се характеризират с фактор на излишък (R)
(1.11)
където - максималното количество информация, което може да съдържа един символ на съобщението, определено по формулата (1.6);
Н — средното количество информация, което носи един знак в реални съобщения;
m— брой знаци в азбуката на източника на съобщението (дължина на азбуката).
Излишъкът показва, че броят на знаците в съобщението е по-голям от необходимия, ако бяха напълно използвани, т.е. при условие че символите изглеждат еднакво вероятни и взаимно независими.
Интересно е да се отбележикоето за европейските езици излишъкът е поне 0,5.