Съвременен подход за диагностика на техническото състояние на потопяемо електрическо оборудване с
Такъв математически апарат позволява да се извършват по-задълбочени изследвания на вибрациите на оборудването, да се локализира сигналът в честотната област, което прави възможно представянето на сигнала под формата на отделни допълнителни компоненти. Тези компоненти имат характерни характеристики за всеки отделен дефект, което позволява не само цялостно да се оцени TS на потопяемото оборудване, но и да се идентифицира вида на дефекта с определена степен на сигурност. Освен това има методи, които позволяват извършване на спектрален анализ с помощта на микропроцесорни инструменти на TMS и избор на необходимата диагностична информация за по-нататъшно предаване към наземната част на системата за подробна обработка [Грешка: Референтен източник не е намерен, Грешка: Референтен източник не е намерен].
Възможността за локализиране на сигнала не само по честота, но и по време се появява при използване на вълновото преобразуване [23, 24, 27, 37]. Основната теория на вълновото преобразуване е описана в [23, 37, 57, 96, 110, 120, 132143]. Аспектите на приложното използване на тази трансформация са разгледани в [24, 27, 41, 59, 80, 85, 96]. Уейвлет трансформацията на сигнал е неговото представяне под формата на серийно разширение по отношение на системата от базисни функции, получена от родителския уейвлетψ(t), посредством операции за мащабиране (a) и времево изместване (b).
Уейвлет е някаква функцияψ(t), за която са изпълнени две условия: средната стойностψ(t)е равна на нула и тя бързо намалява катоt→±∞. Резултатът от вълновото преобразуване на сигналаf(t)е израз, който зависи от два параметъра. Параметърътbопределя времевата локализация на вълната и се нарича отместване, параметърът на мащабаaноси информация за честотата. Дадена е вълновата трансформацияпо следния начин:
(1,0)
къдетоf(t)е зависимостта от времето на вибрационния сигнал;W(a,b)е резултатът от вълновото преобразуване [23, 132].
Трябва да се отбележи следната особеност: стойността на мащабния параметърaе обратно пропорционална на честотата, т.е. колкото по-малък е параметъръта, толкова по-висока е честотата (ω
1/ a ), и обратно, колкото по-голям е параметъръта, толкова по-ниска е честотата
Въз основа на това можем да заключим, че вълновите спектри са подобни на изблици при честотатаω0и лентатаΔω, като тези честоти също намаляват с увеличаване наa. По този начин уейвлетите имат както честотна, така и времева локализация едновременно.
Много различни вълни могат да служат като основа. Когато се използват такива ортогонални бази, е необходимо да се посочат някои свойства, удовлетворяването на които ни позволява да наречем функцията вълна:
Квадратът на нормата на функция трябва да е краен:
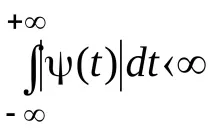
Разликата между вълновото преобразуване и преобразуването на Фурие се крие в оригиналната функция, тъй като в случая на вълновото преобразуване се използва функция, която е едновременно локализирана както в честотната, така и във времевата област.
Площта на графиката на функцията трябва да има стойност, равна на нула:
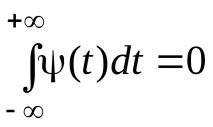
В някои задачи също е необходимо да имаnнулеви моменти:
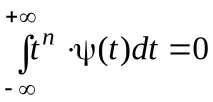
Уейвлетите от по-висок порядък позволяват да се анализират по-високочестотните компоненти на сигнала, като същевременно се потискат други компоненти при по-ниски честоти.
Характерна особеност на вълновото преобразуване е неговото самоподобие.
В рамките на един тип вълни (едно семейство) всички вълни се характеризират с еднакъв брой трептения, поради факта, че всички те са получени сизползване на мащабиране и преместване.
Ефективността на уейвлет преобразуването до голяма степен зависи от метода за избор на основния уейвлет за съответните класове на изследваните функции. Основният критерий за избор на вълна е най-малкият размер на носителя. Освен това външният вид на основната функция трябва да съответства в максимална степен на анализираната функция. В противен случай изборът на вълната се извършва експериментално, въз основа на получените резултати, както и като се вземе предвид времето, изразходвано за трансформацията [68].
Резултатът от разглежданата трансформация съдържа набор от информация, както за изследвания сигнал, така и за приложената вълна. Все пак трябва да се отбележи, че вълновите трансформации все пак позволяват да се извлече информация за изследвания сигнал, тъй като някои от неговите свойства са инвариантни към избора на основната вълнова функция, така че тези свойства са много важни:
Линейносттаследва от скаларното произведение:
Shift. изместването на оригиналния сигнал във времето сb0е придружено от изместване на уейвлет изображението сb0:
Мащабиране. Компресията или разширяването на оригиналния сигнал също съответства на компресията или разширяването на вълновото изображение:
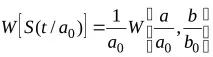
Локализация във времето и мащаба, поради факта, че основната функция е локализирана и има движещ се прозорец време-честота. Чрез промяна на мащаба вълните позволяват да се намерят различни характеристики при различни честоти на сигнала, който се изследва, и поради изместването на времето, може да се изследва сигнала във всяка точка от неговия времеви интервал.
Това обстоятелство определя предимството на вълновото преобразуване пред преобразуването на Фурие, тъй като възможността за едновременна локализация както във времето, така ии в честотната област позволява по-ефективен анализ на нестационарни сигнали.
Нека разгледаме основните типове майчински уейвлети, които най-често се използват в проблеми с приложно уейвлет преобразуване. По принцип това са ортогонални уейвлети с компактна поддръжка (уейвлети на Dabechies, симлет, койфлет и др.). Основните свойства на горните уейвлети са: наличието на компактна опора, наличието на няколко нулеви момента, възможността за извършване на непрекъсната уейвлет трансформация с помощта на бързи алгоритми. Фигура 1.3 показва основните вълни на Daubechies от пети ред (a) и символ от шести ред (b).
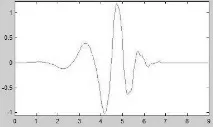
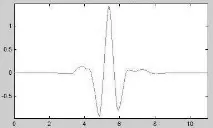
Фигура 1.3 - Примери за уейвлети: Daubechies (a) и symlet (b)
Както показват резултатите от моделирането на вълновата трансформация на сигнал, състоящ се от няколко синусоиди (което е най-често срещаната форма на вибрационния сигнал на ротационните машини), следните видове вълни са най-приемливи за решаване на проблема с вибрационната диагностика:
Wavelet на Daubechies (порядък 5 и по-висок);
симлет (порядък 6 и по-висок);
кофлет (ред 5 и нагоре);
Mayer вълна (дискретна).
Типовете основни уейвлет функции, изброени по-горе, дават приблизително еднакъв резултат от трансформацията и следователно всяка от тях може да се използва за анализ на вибрациите на потопяемо електрическо оборудване [68].
Резултатът от непрекъснатата вълнова трансформация е триизмерна графика (Фигура 1.4.). Мащабният параметърa, времевият параметър (отместване)bи стойностите на вълновата трансформацияW(b, a)са нанесени по координатните оси на тази графика. Трябва да се отбележи, че в практиката най-често се използва двумерното изображение на вълновото преобразуване - скалограмата, която епроекция на вълновото преобразуванеW(b, a)върху равнината(b, a). В този случай различни стойностиW(b, a)се показват чрез интензитет на цвета [59, 60].

Фигура 1.4. - Визуализация на непрекъсната вълнова трансформация
Характеристиките на скалограмите, получени за различни дефекти в потопяемото електрическо оборудване, позволяват да се разработят определени правила за идентифициране на дефекти и определяне на степента на тяхното развитие, което от своя страна служи като основа за синтеза на диагностични алгоритми.
По този начин, въз основа на резултатите от анализа на горните методи за анализ на вибрациите, можем да заключим, че най-обещаващият от тях от гледна точка на проблема с вибрационната диагностика на потопяемото електрическо оборудване е непрекъснатото вълново преобразуване, тъй като най-пълно отразява истинската картина на процесите, протичащи в потопяемото оборудване, които влияят на неговия TS.
Калкулатор
Услуга за безплатна оценка на цената на работата
- Попълнете заявление. Експертите ще изчислят цената на вашата работа
- Изчисляването на цената ще дойде по пощата и SMS
Номерът на вашето приложение
Точно сега по пощата ще бъде изпратено автоматично писмо за потвърждение с информация за приложението.