Свързани контури
Свързани вериги- две вериги се наричат така, ако електрическите процеси, протичащи в едната от тях, влияят на електрическите процеси, протичащи в другата.
Най-простият и в същото време най-често срещаният е индуктивната (трансформаторна) връзка между веригите (фиг. 104, а). E. d. s. E, свързан към първата верига, създава ток I1 в нея. В близост до индуктора L1 се образува променливо магнитно поле, което индуцира e в намотката L2. д.с. взаимна индукция.
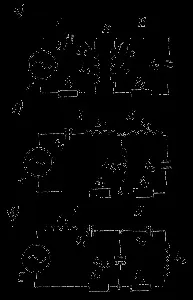
Във втората верига се появява ток I2, създаващ променливо магнитно поле близо до намотката L2, което от своя страна индуцира e. д.с. взаимна индуктивност в първичната верига.
Тъй като намотките L1 и L2 са на известно разстояние една от друга, част от магнитните силови линии на намотката L1 се затварят в околното пространство, като не достигат намотката L2. Степента на влияние на контурите един върху друг се оценява чрез коефициента на свързване Ksv. В случай на индуктивно свързване между вериги, той показва колко пъти e. d.s., индуцирано във втората верига, е по-малко от това e. d.s., който би могъл да се индуцира в него, ако всички магнитни силови линии на намотката L1 участват в създаването му.
Ориз. 104. Схемана свързани вериги: а - индуктивно свързване; b—автотрансформаторна връзка; c - капацитивен съединител.
По този начин коефициентът на свързване винаги е по-малък от едно:
Чрез промяна на разстоянието между намотките можете да промените стойността на коефициента Ksv. В някои случаи тази промяна във връзката между веригите се извършва чрез завъртане на едната намотка спрямо другата с фиксирано разстояние между намотките. С индуктивен куплунг
(160)
Формула (160) ще приеме по-обща форма, ако числителят и знаменателят се умножат по ω:
(161)
И така, коефициентът на свързване между веригите се определя от съотношението на съпротивлението на свързване (Xb) към корен квадратен от произведението на същите реактивни съпротивления на веригата (индуктивни или капацитивни).
На фиг. 104, b показва система отсвързани веригис така наречената автотрансформаторна връзка между веригите, когато взаимното влияние на веригите една върху друга се осъществява чрез индуктора L1,2, който е включен едновременно в двете вериги. В този случай съпротивлението на свързване Хсв = ωL1.2, същите реактивни съпротивления на веригите Х1 и Х2 съответно са равни на co (L1 + L1.2) и co (L2 + L1.2). Заместване на стойностите на Xv, X1 и X2. Във формула (161), след прости трансформации, ние получаваме, по отношение на разглеждания случай на автотрансформаторно свързване, израз за коефициента на свързване:
(162)
Както следва от формула (162), връзката между веригите е толкова по-голяма, колкото по-голяма е индуктивността L1,2.
При капацитивно свързване между веригите тяхното взаимно влияние един върху друг се осъществява чрез кондензатор C1.2, който е включен едновременно в двете вериги (фиг. 104, c). При определяне на коефициента на свързване, както и преди, записваме изрази за Хсв, X1 и X2:

Замествайки тези стойности във формула (161), получаваме, във връзка с разглеждания случай на капацитивно свързване, израз за коефициента на свързване:
(163)
Горните три начина за комуникация между вериги са най-простите. В практиката се използват и други, по-сложни, комбинирани видове комуникация. За удобство при анализиране на работата насвързани вериги, те обикновено се заменят с една еквивалентна схема. В този случай всички изводи, направени по отношение на една верига, се отнасят за всяка сложна система от свързани вериги.
Като пример, разгледайте случаяиндуктивно свързване между вериги (виж фиг. 104, а). Използвайки втория закон на Кирхоф, можем да напишем следните уравнения:
Решавайки второто от горните уравнения за тока I2 и замествайки стойността му в първото уравнение, получаваме
След прости трансформации имаме:
(164)
Тук изразът в квадратни скоби е съпротивлението на еквивалентната верига Z1e, т.е. съпротивлението на първата верига, като се вземе предвид влиянието на втората верига върху нея;
R1 е активното съпротивление на първичната верига; - въведено активно съпротивление от втората верига към първата; X1 е реактивното съпротивление на първичната верига; - въведено реактивно съпротивление от втората верига към първата.
По този начин систематаот свързани веригиможе да бъде заменена от еквивалентна последователна верига под формата на последователно свързване на активното и реактивното съпротивление на еквивалентната верига:
Токът в първата (еквивалентна) верига може да се определи по формулата
(165)
Влиянието на втората верига върху първата се изразява в увеличаване на активните загуби в първичната верига и промяна на нейното реактивно съпротивление. Активното съпротивление на еквивалентната верига винаги е по-голямо от активното съпротивление на първичната верига, а реактивното съпротивление на еквивалентната верига зависи от знаците на X1 и X2. Резонансът в еквивалентната верига (в свързани вериги) възниква при X1e = 0.
Взаимното влияние на контурите може да се обясни и с помощта на векторната диаграма, показана на фиг. 105.
Векторната диаграма е конструирана за случая, когато и двете вериги са настроени на честотата e. резонансната честота на първата верига ω01 е равна на резонансната честота на втората верига ω02 и двете съвпадат с честотата на външния e. д.с.
Фиг.105. Векторна диаграма на свързани контури.
От векторната диаграма се вижда, че токът в първичната верига е във фаза с външната е.д.с. с. Това се дължи на факта, че съпротивлението на веригата, настроена на резонанс, е активно. Токът I1 индуцира e. д.с. взаимна индуктивност в бобина L2:
От последния израз следва, че EM2 е извън фаза с I1 с 90°. Токът във втората верига I2 индуцира в първата верига e. д.с. взаимна индуктивност EM1, която изостава от тока с 90 ° във фаза.
От векторната диаграма също се вижда, че външното e. д.с. E и e. д.с. взаимна индукция EM1 са в противофаза. Последното причинява намаляване на тока в първичната верига:
тъй като външният e. д.с. трябва да преодолеят противоположното e. д.с. ЕМ1.
Подобно заключение може лесно да се стигне с формула (165).
Наистина, когато и двете вериги са настроени на резонанс, т.е. когато X1 \u003d 0 и X2 \u003d 0, токът в първата верига
Влиянието на втората верига върху първата се отразява под формата на увеличаване на съпротивлението на първата верига със стойността на въведеното съпротивление Rin, което води до намаляване на тока в първата (еквивалентна) верига.
Условието за резонанс за случая на индуктивно свързване между вериги може да бъде написано, както следва:
Ако пренебрегнем R2, тогава реактивното съпротивление на еквивалентната верига ще бъде равно на
След прости алгебрични трансформации и заместване на C1 през 1/L1ω 2 0, C2 през и 1/L2ω 2 0 през K 2 st, крайното уравнение за X1e приема формата
Това уравнение за честотата w има два корена:
От последните изрази следва, че еквивалентната верига и следователно системата от свързани вериги има две честоти, съответстващи на резонанса, при които токът в еквивалентната верига е най-голям.Колкото по-голяма е връзката между веригите, толкова повече ω'0 (ƒ'0) и ω''0 (ƒ''0) се различават от резонансната честота, на която всяка от веригите е настроена отделно.