Техники за решаване на задачи на LP с помощта на MS-Excel - Studiopedia
Нека да разгледаме по-сложни примери за задачи на LP, с голям брой променливи за вземане на решения, което ще ни позволи да демонстрираме допълнителни техники, които са полезни при изучаването на модели на линейно програмиране.
Мини-калъф "Планове за обществени поръчки"
Мисия #3: В сладкарската фабрика.
Малка фабрика за сладкарски изделия трябва да затвори за реконструкция. Необходимо е да се продадат останалите запаси от суровини за производство на сладкиши от асортимента на фабриката, като се получи максимална печалба. Запасите и потреблението на всеки вид суровина за производството на единица продукция от всеки вид, както и получената печалба от това са представени в таблица 1.6. Бригадирът, използвайки богатия си опит, предлага да произведе 200 опаковки от всеки вид бонбони от асортимента, като се аргументира, че трябва да има достатъчно ресурси и печалбата ще бъде 1080 USD. Млад мениджър, току-що завършил икономически институт, твърди, че подобни проблеми не се решават на око, а с помощта на линейно програмиране.
Собственикът на фабриката обещава на мениджъра всички печалби над $1080, ако той излезе с по-добър план от много опитния майстор. Ще въведем всички параметри в таблица 8.
Основните параметри на задачата "Във сладкарската фабрика"
Математически модел на задача No3. За променливи на решение ще вземем броя на опаковките на всеки от 5-те вида сладкиши, произведени от фабриката.
Нека ги обозначим като Xi, i=1,2,3,4,5. Тогава целевата функция, печалбата от производството на даден брой опаковки от всеки вид продукт, ще бъде равна на
Ограничения върху променливите: потреблението на всеки вид суровина (в kg) за производството на една опаковка от всеки продукт може да се намери в пресечната точка на реда (суровина) и колоната (продукт) в таблицата с параметри. Това са така наречените технологичнипроизводствени темпове.
Консумацията на тъмен шоколад за опаковки X1 на всеки от техните продукти не трябва да надвишава предлагането на този ресурс. Тези. ограничението за черен шоколад ще изглежда така:
По същия начин можете да получите ограничения за други ресурси, освен това от икономическия смисъл на проблема следва, че всички Xi≥0.
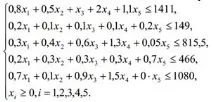
Решение на мини казуса "Във сладкарската фабрика" с помощта на MS-Excel
Ние организираме данните в листа на MS-Excel, както е показано в таблица 9.

Клетки C13 до G13 съдържат променливи за вземане на решения. В клетки B16 до B20 се въвеждат формули, които отразяват потреблението на ресурси за единица от всеки продукт. След като повторихме алгоритъма за решаване на проблема с помощта на MS Excel, получаваме решението. След командата "Изпълни" в клетки от C13 до G13 (Таблица 10) можете да прочетете отговора. Тъй като броят на произведените пакети трябва да бъде цели числа, стойностите на получените променливи трябва да бъдат закръглени до цели числа, така че ограниченията на ресурсите да се спазват стриктно. Клетки C13 до G13 съдържат разходите за ресурси, необходими за получаване на оптималния план.
Резултатите от решаването на проблема "Във сладкарската фабрика"

След решаването на проблема с оптималния план за фабрика за сладкарски изделия, младият мениджър изпита двойствено чувство. От една страна, печалбата, съответстваща на намерения от него производствен план, е почти $430. повече отколкото според плана на господаря, т.е. той спечели повече от 400 USD, от друга страна, любимият му „Бар“ не беше включен в оптималния план. Как да оправим ситуацията. Мениджърът трябва да отговори на следните въпроси:
1. Как трябва да се промени нормата на възвръщаемост за "Бар", така че да влезе в оптималния план?
2. Ако въведем тази промяна в данните и решим проблема отново, как ще се промени оптималният план?
3. Кой ресурс е най-оскъден (т.е. има най-голямо въздействие върху печалбите)?
4. Може ли да се каже (без да се решава отново задачата) как ще се промени печалбата от производството, ако количеството на този ресурс се оцени: а) с излишък от 10 тегловни единици; б) с дефицит от 5 единици?
5. Има ли друг начин за постигане на производството на "Bar", освен промяна на нормата на печалба?
За да се отговори на тези въпроси, е необходимо да се получи MS-Excel доклад за устойчивост (Таблица 11).
Доклад за устойчивост на MS Excel на задачата "Във сладкарската фабрика"

Отговор на въпроси 1 и 2. Според доклада за устойчивост (Таблица 10) нормализираната цена на бонбона „Батончик“, който не е включен в оптималния план, е 0,00874 куб. Абсолютната стойност на това число показва колко е необходимо да се увеличи печалбата от една опаковка от тези сладки, за да влезе "Батончик" в оптималния план. За да направите това, нека решим проблема отново, като променим един параметър, а именно, като увеличим цената на „бара“ с 0,01 c.u. В този случай печалбата ще бъде равна на 1.11.u. (Таблица 12).
Таблица 1.12. Оптималният план за задачата „Във сладкарската фабрика“

Виждаме, че малки промени в параметрите водят до сериозни промени в решението. За сравнение, под печалбата се записват резултатите със същата цена за “Батончик”. В този случай се казва, че решението на проблема е нестабилно.Решението се нарича нестабилно,ако малки промени в параметрите водят до огромни промени в решението. Тази нестабилност е особено опасна, когато се разглеждат методи за избор на решение под риск. В нашата задача печалбата и в двата случая е почти еднаква, т.е. нестабилността на решението не е ужасна. Ако въведете целочислени ограничения за броя на опаковките от всеки тип продукт или изисквате ограничение:броят на пакетите „Bar“ беше поне 100, 200, 300, ще получим алтернативни решения, които се различават значително в стойностите на променливите, но са много близки по печалба. Това е добре, защотоналичието на много „добри“ алтернативни решения позволява на мениджъра да избере това, което най-добре отговаря на определени условия, които винаги присъстват при вземането на решения.
Отговор на въпроси 3 и 4. За да отговорим на тези въпроси, нека разгледаме доклада за устойчивост (Таблица 11). Според него най-висока цена в сянка има ресурсът „лек шоколад“. Но интервалът на стабилност, съответстващ на тази цена, е много малък (149-11.87; 149+1.04). Ако запасът от този ресурс се намали с 10 единици, тогава реалната печалба ще бъде по-ниска:
Тази формула може да се използва, тъй като Δb2=-10 попада в интервала на стабилност. Ако предлагането на даден ресурс се увеличи с 5 единици, е невъзможно да се предвиди увеличение на печалбите, т.к Δb2=5 надхвърля интервала на стабилност. В този случай проблемът трябва да бъде решен отново.
Отговор на въпрос 5. Необходимо е да се обърне внимание на факта, че всеки от ресурсите за производство на "Батончик" е оскъден и се търси от друг продукт. Батончик се състезава с Белка за ресурси: захар и ядки. Потреблението на тези ресурси за тези два продукта е най-голямо. Увеличаването на запасите от тези ресурси може да доведе до влизане на "Батончик" в оптималния план. Така че, ако увеличите запасите от захар с 40 единици. и преразрешим проблема максимално, получаваме нов оптимален план, при който ще бъдат произведени повече от 1080 опаковки „Бар“, докато печалбата ще бъде P=1547,8 c.u. 23
В прозореца „Добавяне на ограничение“ има опция за изискване променливите на решението да бъдат цели числа. За да направите това, изберете ограничението “target” от предложените ограничения. РешениеZLP в Excel прави невъзможно получаването на информация за стабилността на решението и за сенчестите цени. Следователно „Търсене на решение“ MS Excel не генерира отчет за стабилност, ако условието за цяло число е въведено за поне една променлива. Нека разгледаме проблема.
Не намерихте това, което търсихте? Използвайте търсачката: