Теореми за равенство и подобие на триъгълници - ТРИЪГЪЛНИЦИ - МАТЕМАТИКА - Формули и таблици

Триъгълник - където е многоъгълник с три страни. Страните на триъгълника са обозначени с малки букви, които съответстват на обозначението на противоположните върхове.

Ако и трите ъгъла са остри, тогава триъгълникът е остър. Ако един от ъглите е прав - правоъгълен; страните, които образуват прав ъгъл, се наричат ​​катети (a и b), страната срещу правия ъгъл е хипотенузата (c). Ако един от ъглите е тъп, триъгълникът е тъп.

Триъгълник ABC е равнобедрен, ако две от страните му са равни (a = c); равностранен, ако трите му страни са равни (a = b = c). Равните страни на равнобедрен триъгълник се наричат ​​странични, третата страна се нарича основа.

Във всеки триъгълник има по-голям ъгъл срещу по-голямата страна; срещуположни равни страни - равни ъгли и обратно.

Равностранният триъгълник има равни ъгли и обратното: ако ъглите на триъгълника са равни, значи той е равностранен.

Във всеки триъгълник сборът от ъглите е 180°

Теореми за равенствоиподобие на триъгълници

Два триъгълника са подобни, ако:

- страните им са съответно пропорционални;

- ъгли на два триъгълника според нивото;

- двете страни на едната са съответно пропорционални на двете страни на другата, ъглите между тях са равни

Правоъгълните триъгълници са подобни, ако хипотенузата и катетът на единия триъгълник са пропорционални на хипотенузата и катета на другия

Триъгълниците са еднакви, ако

- страните на един триъгълник, съответно нивата на страните на втория;

- съответно двете страни и ъгълът между тях са равни;

- едната страна и прилежащите й ъгли на 1-вия триъгълник са равни на страната и ъглите на другия триъгълник.

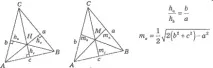
Всяка страна на триъгълник е по-малка от сбора и по-голяма от разликата на другите две.страни:

a c + b; a > в - б

Височината на триъгълника е перпендикулярът, пуснат от който и да е връх на триъгълника към противоположната страна или нейното продължение.

Пресечната точка на трите височини на триъгълник се нарича ортоцентър. В тъп триъгълник ортоцентърът е извън триъгълника, в правоъгълен триъгълник съвпада с върха на правия ъгъл

Медианата на триъгълник е сегмент, който свързва който и да е връх на триъгълника със средата на противоположната страна. Три медиани на триъгълник се пресичат в една точка (винаги в триъгълник), която е центърът на тежестта (масата) на триъгълника

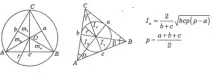
Симетралата на триъгълник е отсечката от ъглополовящата на произволен ъгъл от върха до пресечната точка с противоположната страна

Трите ъглополовящи на триъгълник се пресичат в една точка (винаги вътре в триъгълника), която е центърът на вписаната окръжност

Симетралата разделя противоположната страна на части, пропорционални на съседните страни.

Симетралата разполовява ъгъла. Височината пада на противоположната страна под прав ъгъл

Медианата разделя триъгълника на два равни триъгълника. Медианата разполовява противоположната страна

Средният перпендикуляр на отсечка е права линия, която минава през средата на отсечката, перпендикулярна на нея

Три средни перпендикуляра към страните на триъгълника се пресичат в една точка, която е центърът на окръжността, описана около триъгълника

---