Трифиларна теория на окачването
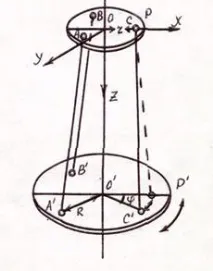
Схемата на трифиларното окачване е показана на фигура 6.
Подвижната платформа P' е окачена на платформата P на три симетрично разположени нишки AA', BB'. , CC'. -P платформата ви позволява да се вълнувате. система за торсионни вибрации. Ротационният импулс, необходим за започване на торсионни вибрации, се предава на платформата от специално устройство, което се намира отгоре на устройството, което задвижва лоста, свързан с диска. Така се постига почти пълната липса на други торсионни вибрации, чието наличие затруднява измерванията. За удобство при отчитане на трептенията на платформата има маркировка, срещу която, когато платформата е в покой, се поставя показалец - тел на статив.
Когато долната платформа P' (спрямо горната) се завърти около вертикалната ос на определен ъгълj, възниква момент на сили, който се стреми да върне платформата в равновесно положение. Ако триенето се пренебрегне, тогава на базата на закона за запазване на енергията за трептяща система можем да запишем: , (1)
където е кинетичната енергия на системата, е потенциалната енергия на системата,Iе инерционният момент на платформата заедно с изследваното тяло,Mе масата на платформата с тялото,z0е началната координата
точка O' (при(j=0),z- координата на точка O при текущата стойностj. Точката означава диференциране по отношение на времето.
Както следва от фиг. 1., координатите на точка C в координатната система (x,y,z) са (r,0,0), а точката C' има координати (Rcosj0 ,Rsinj0, Z), където j0 е максималния ъгъл на отклонение. Разстоянието между точките C и C’ е равно на дължината на нишкатаl, Записвайкиlчрез стойността на нейните координати (l 2 =x 2 +y 2 +z 2, къдетоx 2 =(Rcosj0-r) 2 , y 2 =(Rsinj0) 2 , z 2 =z 2, получаваме:
(R cosj0 - r) 2 + (R sinj0) 2 + z 2 =l2
тъй катоZ 2 =l 2 -(R-r) 2 = l 2 -R 2 +2Rr-r 2.
Като се има предвид, че за малки ъгли на отклонениеj0 cosj0 » 1-j0 2 /2получаваме
Приравнявайки корена на израз (2), намираме, че при малки ъглиj
(3)
От (3) следва, че , (4).
защотоZ0=l. Ако приемем, че платформата извършва хармонични трептения, можем да запишем зависимостта на ъгловото преместване във формата:
, (5)
къдетоj0- амплитуда на отклонение,Т- период на трептене,t- текущо време. Ъгловата скорост, която е първата производна по отношение на времето, се изразява, както следва: (6)
В момента на преминаване през равновесното положение
абсолютната стойност на това количество ще бъде
, (7)
Въз основа на горното (изрази (1) и (7)) имаме
(8)
Замествайки израз (4) в (8), получаваме
откъде (9)
Съгласно формула (9) може да се определи инерционният момент на платформата и тялото, поставено върху нея, тъй като всички количества от дясната страна на формулата могат да бъдат директно измерени. Формула (9) е валидна при липса на
система от загуби на енергия поради триене, или приt>>T, къдетоTе периодът на трептене на системата, аtе времето, през което амплитудата на трептенията на платформата значително намалява (с 2-3 пъти).
Параметри на трифиларното окачване.
2R3 = 0.12 m;m0= (0,481+0,01) kg - тегло на празната платформа.