управляемост и наблюдаемост
Помислете за две основни свойства на системите за управление, които са толкова важни, колкото и свойството за стабилност. Първият от тях е свързан с възможността за прехвърляне на системата от произволно първоначално състояние във всяко друго дадено състояние, а вторият е с възможността за определяне на състоянието на системата чрез контролираната стойност и управляващото действие.
Определение за управляемост. Система (управлявана система или обект) с уравнение на състоянието
(1)
енапълно контролиран, ако има управляващ сигналf, който прехвърля системата от нулево начално състояниеx(0)=0 в моментаt0=0 към всяко друго състояниеx(tf) за крайно времеtf.
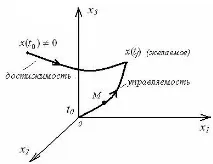
Тук точкатаMе представителна точка.
Промяната на позицията на изобразителната точка е преходът на системата от едно състояние в друго.
Лесно е да се покаже, че ако системата е напълно управляема, тогава при определени предположения тя може да бъде прехвърлена отвсякопървоначално състояние във всяко друго състояние. Това свойство на системата се наричадостъпност.
Управляемостта е частен случай на достижимост.
Фигурата по-горе дава геометрична интерпретация на свойствата на управляемост и достижимост.
Теорема на Калман. (За пълна контролируемост).
За пълна управляемост на системата, описана с уравнение (1), е необходимо и достатъчно матрицата на управляемост (блокова матрица)
(2)
имаше ранг равен наn, къдетоnе редът на системата:. МатрицатаUима измерение (), тъй като всеки блок има измерение и има общоnблока (колони).
Ако има поне един второстепененn-ти ред на матрицатаU, тогава .nвторостепенният ред е детерминантата наUматрицата, съставена отnпроизволни колони наUматрицата.
За система с един вход, т.е. ако , тогаваUе квадратна матрица и има единствен минор отn-ти ред, който съвпада с детерминантата на матрицата. В този случай условието за пълна управляемост заr=1:
,
тоест матрицата на управляемост трябва да бъде неизродена.
Пример.За двоен интегратор
,
къдетоkе печалбата на двойния интегратор.
Двойният интегратор може ли да се контролира напълно и при какви условия?
В този случайn=2,. Следователно, в съответствие с (2), матрицата на управляемост на двойния интегратор
,
.,
Следователно, ако . Това е условието за пълна управляемост на двойния интегратор.
Команди на Matlab:U=ctrb(A,B); r=ранг(U).
Забележка 1. Физическият смисъл на свойството пълна управляемост е, че управлението засяга всяка от променливите на състоянието , . В този случай е възможно произволно да се промени позицията на представителната точка с помощта на подходящ контрол.
Забележка 2. Дали системата е напълно управлявана може да се определи с помощта на оперативната блокова диаграма. Ако операционната блокова диаграма има пътища, водещи от контрола до всяка променлива на състоянието, тогава системата е напълно управляема.
Пример. Разгледайте оперативната блокова диаграма на системата, показана на фигурата по-долу. Тук ,n=2.
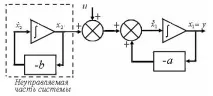
Както можете да видите, контролатаuще засегне само променливатаx1. Лявата част на блоковата диаграма се държи автономно от управлениетоu. Следователно системата не е напълно контролируема. Ако системата не е напълно управлявана, тогава тя може да бъде разложена на управлявани и неуправляеми части (подсистеми).
Нека покажем аналитично, че разглежданата система не е напълно управляема. За да направим това, според блоковата диаграма намираме уравненията в променливи на състоянието
от което се вижда, че управлениетоuне влияе наx2 .
, .
Оттук и матрицата на управляемост
.
Както можете да видите, , тоест системата не отговаря на условието за пълна управляемост.
Забележка 3. Ако система с един вход, с други думи, заr=1, не е напълно управляема, тогава нейната PF се изражда, с други думи, нейната PF е изродена PF, тоест редът на PF знаменателя ще бъде по-малък от реда на системата (реда на характеристичното уравнение на системата).
Следователно система с един вход е напълно управляема, ако нейната предавателна функция не съдържа същите множители в числителя и знаменателя (отменими множители).
За примера, обсъден в Забележка 2:
, ,l=1.
В този случай PF на системата
,
където е характеристичният полином
.
Следователно корените на характеристичното уравнение = 0, с други думи полюсите на системата са равни: .
Намерете числителя, който е скаларен полином
.
.
Редът на системата еn=2,и редът на PF знаменателя е 1, т.е. трансферната функция на системата е изродена. Тази система е стабилна при начални условия, ако (влявокорени). Ако , ( е десен корен), тогава системата е стабилна на вход и нестабилна на начални условия.С други думи, компенсирането на десните (без минимална фаза) нули на системата поради полюсите на друга система, свързана последователно, прави последователната връзка нестабилизирана.
Моделът PF може да бъде само частично описание на системата.
Забележка 4. Системата, описана с уравнение (1), се наричастабилизираща, ако неконтролираната част е стабилна при начални условия. За примера, разгледан в Забележка 2, условието за стабилизиране на системата е: .
Свойството на стабилизация позволява, благодарение на обратната връзка, да се осигури стабилността на затворена система, дори когато обектът на управление съдържа неконтролирана част. Включването на неуправляема част в системния модел е доста общ случай. Това е удобно за описание на различни смущаващи влияния. Например, постоянно смущаващо действие може да бъде определено в пространството на състоянието като .
Забележка 5. Рангът на матрицата на управляемост не зависи от избора на вектора на състоянието. С други думи, рангът на матрицата на управляемост е инвариант, т.е.
,
=TU
е матрицата на управляемост на трансформираната система, описана от
.