Времево квантуване на сигнали
Курсов проект по дисциплината "Теория на информацията и сигналите"
Завършено от студент от група 03-CT-11 от курса на 3-ти факултет на CTAS
Кубански държавен технологичен университет
Катедра по ВТ и ОКС
В наши дни информацията се е превърнала във фактор, който определя ефективността на всяка сфера на дейност. Увеличиха се информационните потоци и се увеличиха изискванията към скоростта на трансфер на данни, един от факторите за увеличаване на скоростта на трансфер на данни е методът на дискретизация на сигналите във времето, т.е. при предаване на сигнал е възможно да се предава не целия сигнал, а само неговите отчети и да се възстанови сигнала според отчетите. В този случай се предават само импулси (щраквания), а на приемника тези щраквания възстановяват сигнала
В работата е реализиран алгоритъм за квантуване на сигнали във времето.
Съобщението, представено от електрически сигнал, трябва да бъде предадено на определено разстояние (включително достатъчно голямо). За целта се използват сигнали – носители. Енергията на носителите трябва да е достатъчна за предаване на дадено разстояние.
По този начин трансформацията на сигналите по време на предаване се състои в въздействие върху носителя, променяйки един или друг от неговите параметри. Този ефект се нарича модулация.
Различните видове модулация се характеризират с различни видове носители, както и с редица параметри, които подлежат на промяна.
Според вида на носителите има:
модулация на синусоидални (хармонични) сигнали;
модулация на импулсни сигнали.
Според параметрите, които трябва да се променят, има:
кодова модулация и др.
В случаите, когато непрекъснато съобщение се предава в дискретна (цифрова) форма, се извършва предварително преобразуваненепрекъснато съобщение в дискретно, включително дискретизация (квантуване) по време и ниво.
В най-новите системи за предаване на информация, особено в многоканалните системи с времево мултиплексиране (разделяне) на каналите, носителят е последователност от правоъгълни импулси. С такъв носител могат да се променят следните параметри: амплитудата на импулсите, тяхната ширина, честота на повторение, позиция или фаза и кодовете, образувани от тях. Съответно се разграничават следните модулации:
амплитудно-импулсна модулация AIM;
широчинно-импулсна модулация ШИМ;
времеимпулсна модулация VIM;
позиционно-импулсна модулация (фаза-импулс) PIM (PIM);
честотно-импулсна модулация PFM;
импулсно кодова модулация CIM.
При предаване на непрекъснати съобщения в информационните системи, импулсно-кодовата модулация (CMM) на сигналите стана много широко използвана. CIM се състои от три операции:
дискретизация на сигналите във времето;
дискретизация на сигналите по ниво;
Времевата дискретизация се състои в замяна на непрекъснатия във времето сигнал X(t) с дискретен сигнал, чиито стойности за дискретни времена t съвпадат съответно с моментните стойности на непрекъснатия сигнал. Тази операция се нарича също времево квантуване на сигнала.
Дискретизацията на нивото (квантуване на ниво) се състои в замяна на непрекъснат набор от стойности на сигнала X(t) с набор от дискретни стойности. В този случай скалата на възможните стойности на сигнала се разделя на определен брой интервали и непрекъснатата стойност на сигнала се заменя с най-близката дискретна. След това получените дискретни стойности се кодират (обикновено в двоичен код).
PWM (импулсна кодова модулация) осигурява значително увеличениешумоустойчивост на предаване на съобщения. В допълнение, дискретизацията на времето прави възможно използването на едни и същи устройства (комуникационни канали, устройства за обработка на информация и т.н.) за голям брой различни сигнали.
При CMM е много важно да изберете правилния метод за квантуване на сигнала по отношение на времето и нивото. В тази връзка нека разгледаме някои въпроси от теорията за квантуване на непрекъснати функции по време и ниво.
Когато се квантува във времето, непрекъснатата по аргумент функция x(t) се трансформира във функция
Честотата на квантуване трябва да бъде избрана по такъв начин, че да е възможно да се получи оригиналната функция от референтните стойности x(ti) с дадена точност.
Има няколко критерия за избор на честотата на квантуване във времето. Тези критерии включват по-специално честотния критерий на V.A. Котелников. Този критерий, наречен теорема на V.A. Котелников, се основава на следния сигнален модел:
сигналът е стационарен случаен процес;
спектърът на сигнала е непрекъснат и ограничен до определена честота, отвъд която е идентично равен на нула.
Теорема V.A. Котелников: ако непрекъсната функция x(t) удовлетворява условията на Дирихле (ограничена, непрекъсната на части и има краен брой екстремуми) и нейният спектър е ограничен от определена честота fc, тогава тя се определя напълно от показанията, разположени на разстояние
За да докажем теоремата, разглеждаме изразите за прякото и обратното преобразуване на Фурие на непрекъсната функция x(t).
В конкретния разглеждан случай могат да се изпишат функции с ограничен спектър
Ще допълним функцията до периодична с период равен на 2fc (Фигура 1) и ще я разширим в серия на Фурие
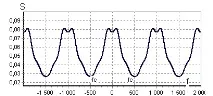
Фигура 1 - функция с период равен на 2fc.
Сравняванеизрази (3) и (5), отбелязваме, че те съвпадат с точност до постоянен множител
Заместване на намерения израз за
След заместване на (6) в (3), промяна на знака при k (тъй като сумирането се извършва върху всички положителни и отрицателни стойности на k) и пренареждане на операциите за сумиране и интегриране, получаваме
След като заместим (8) в (7), най-накрая получаваме
Полученият израз представлява аналитично теоремата на Котелников.
От (9) се вижда, че непрекъснатата функция X(t) (Фигура 2, а), която има ограничен спектър, може да бъде представена чрез разширяване в серия, всеки член от която се изразява чрез една и съща функция под формата sin(x)/x (референтна функция), но с различни коефициенти
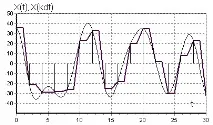
Фигура 2, а - Функция за броене
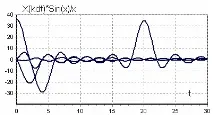
Фигура 2, b - Референтна функция, но с различни коефициенти
Серия (9) е декомпозиция на случаен процес с координатни функции (детерминистични функции на времето) и коефициенти на тегло