Заблуди на логическото мислене в математиката Теми за дискусия (M)
Заблуди на логическите разсъждения в математиката
Много често хората, като спорят сякаш логично, стигат до неправилни заключения. Намирането на грешка в логиката е трудно. И дори ако мястото на грешката е интуитивно ясно, е трудно да се обясни твърдо.
Все още се интересувам от грешката, свързана с разсъждения като "когато нещо клони към безкрайност, нещо клони към някаква граница." Къде са ясните правила, по които може да се използва тази фраза? Ако няма такива правила, те ще го използват навсякъде, стигайки до грешни резултати.
Например има такава задача: да се докаже, че сборът от катетите на произволен правоъгълен триъгълник (евклидов) е равен на хипотенузата.
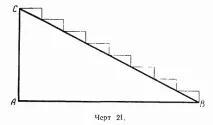
Нека вземем произволен правоъгълен триъгълник и разделим хипотенузата му на равни части, където е някакво естествено число, и след това начертаем двойка прави сегменти през всяка точка на делене, единият успореден на единия катет, другият успореден на другия катет. Продължавайки тези сегменти, докато се пресекат извън триъгълника, получаваме стъпаловидна начупена линия, показана на чертежа. Сумата от дължините на всички връзки на тази прекъсната линия е равна на сумата от краката, тъй като сумата от всички начертани сегменти, успоредни на един от краката, е равна на този крак.
Сега ще увеличаваме числото безкрайно, като му даваме последователни стойности и т.н. Броят на връзките в нашата прекъсната линия ще нараства неограничено (той е равен на), но дължината на всяка връзка ще клони към нула и прекъснатата линия ще се различава все по-малко от хипотенузата. В границата при , начупената линия ще се слее с хипотенузата и следователно дължината на начупената линия в границата ще бъде равна на дължината на хипотенузата. Но дължината на цялата прекъсната линия е равна на сбора от катетите. Така че дължината на хипотенузата е равна на дължината на катета.
Подчертах с удебелен шрифтмястото, където открих това, което според мен е грешка в логическите разсъждения. Но не мога да го обясня, защото не видях ясни правила за прилагане на тези формулировки. Изправен съм пред следната опозиция:
В учебника по математически анализ.
От факта, че максималното разстояние между две криви (в този случай хипотенузата и полилинията) клони към нула, не следва, че дължините на тези криви клонят една към друга.
Покажи поне един учебник по математически анализ, където се пишат такива глупости.
Няма много да се слеят. Това не означава, че някои характеристики ще се слеят. Това изисква допълнителни основания. например:
Използвайки концепцията за границата на последователност от начупени линии, трябва да докажем следната теорема: Границата на дължините на начупените линии е равна на дължината на границата на начупените линии. Тази теорема има формата . В хода на математическия анализ се доказват няколко теореми от този вид. Но това не означава, че всички подобни теореми са верни за всякакви функции и всякакви последователности. Трябва да докажете тази теорема.
След изпълнението на тази програма ще може да се каже, че разсъждението е правилно. Но няма да можете да го направите. Доказателството на последната теорема изисква такива свойства от последователността от многоъгълни линии, които трионът от примера няма, но например правилните многоъгълници, вписани в окръжност, имат.
Някои от отговорите са достойни. Намерих обяснение на този проблем в Errors in Mathematical Reasoning (1959), което ще копирам по-долу. ------------------------------
Подмяна на точните дефиниции с геометрична интуиция.
Доказателството на всяко математическо съждение трябва да се основава: на първични понятия, на точни дефиниции на всички други понятия, аксиоми, предварително доказани теореми от дадена научна област и само на тях. Дефиниции Премахваненесигурността на използваните понятия (термини), което често причинява различни погрешни схващания. Добре известното правило на Паскал (1623-1662) предупреждава, че за проверка е необходимо да се заменят дефиниции с термини.
Грешките обаче често възникват от опитите на учениците да установят някакви данни от опит, извлечени от визуално изображение, като допълнителни основания за доказателство. Това породи в средата на миналия век сред изявените умове на аналитичния склад тенденция за изхвърляне на чертежа от математиката.
Съзерцаването на рисунката прави силно впечатление на начинаещите в изучаването на математика. То действа като безспорен факт, който само трябва да намери подходящо обяснение. Дори учениците, под влиянието на визуален образ, понякога са склонни да забравят за точните дефиниции на определени понятия, особено когато визуалното впечатление, изглежда, напълно дава пряк отговор на поставения въпрос, без да изисква косвена проверка.
Така че разглежданият въпрос е доста сложен, а правилното му разбиране има изключително голямо идейно-възпитателно значение. Последното се улеснява от анализа на специално подбрани примери, изградени върху прекомерно доверие в геометричната интуиция, която, изглежда, действа като еквивалент на съответните точни определения. Може би това се отнася особено за прилагането на концепцията за лимит. Софизмите по тази тема са отразени и в някои методически обработени учебници по математически анализ.
Пример. Сборът от катетите е равен на хипотенузата.
В горните разсъждения се допуска произволен извод: от желанието на прекъснатата линия да се слее с хипотенузата в смисъла, както е посочен в текста, няма основание да се заключава, че границатаДължината на прекъснатата линия е дължината на хипотенузата. Така това предположение остана неоснователно. Не може да се докаже, защото е невярно. Всъщност тук не се намираме в условията на приложимост на понятието граница: разликата между променлива, в частния случай константа (дължината на прекъсната линия), и нейната предполагаема граница (хипотенуза) не е нито безкрайно малка стойност, нито нейният частен случай - нула.