Задача 4

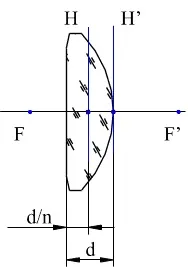
За лещите с една плоска повърхност се определя едно свойство, което следва от съотношенията за параксиални характеристики: основната равнина преминава през върха на неравнинната повърхност.

Другата главна равнина е на разстояние d/n от плоската повърхност.

Коефициентите за други лещи от този тип са лесни за определяне, така че можете да го направите сами.

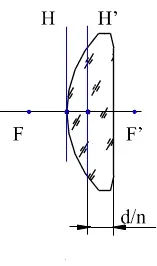
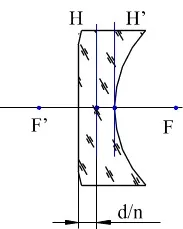
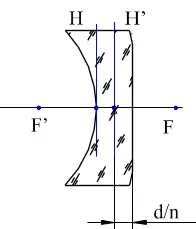
Обект от 5 mm се поставя на 150 mm пред леща с изпъкнала равнина с радиус на повърхността 50 mm, дебелина 10 mm и индекс на пречупване 1,5. Определете размера и позицията на изображението спрямо последната повърхност S'.

Първо, необходимо е да се определят параксиалните характеристики на системата. В съответствие с горните отношения имаме: f'=100; SH=0; S'H=-6,67.

Това означава, че в нашия пример a=s=-150.

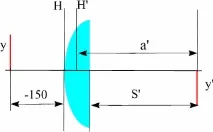
Позиция на изображението

a'=300, така че S'=SH'+a'=293,33 mm

β=-f/z, където z=S-Sf=s-f=150-(-100)=-50 mm.

Отговор:S'=293,33 mm, y'= -10 mm.

Също така, пример за изчисляване на позицията / увеличението на обект / изображение може да се види в примера за изпълнение на "Лабораторна работа № 2. Определяне на параксиалните параметри на свързана леща".

Намерете коефициента на пречупване на плоско-вдлъбната леща, ако оптичната сила е Ф = -12,50 диоптъра. Радиусът на повърхността по абсолютна стойност е 40 mm.

Оптичната сила на лещата зависи от индекса на пречупване:

Показател на пречупване: n=1-Ф r2=1-(-0.0125 40)=1+0.5=1.5

Практически урок номер 4. Определяне на параксиални параметри на различни видове лещи

4.3. Определяне на параксиалните параметри на менискусни лещи

Следва описание на структуратапараметри на оптичните елементи, достатъчни за определяне на типа. Трябва да се отбележи, че в някои задачи типът на лещата е даден, за да се определят знаците на проектните параметри.

Конвексно-вдлъбнат събирателен менискус (положителен)

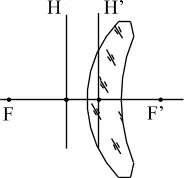
Конвексно-вдлъбнат разпръскващ менискус (отрицателен)

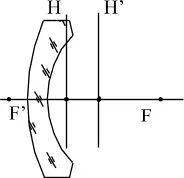
Вдлъбнато-изпъкнал събирателен менискус (положителен)

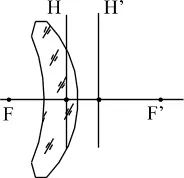
Вдлъбнато-изпъкнал разпръскващ менискус (отрицателен)

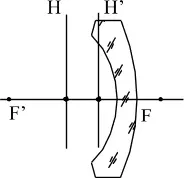
Изображението е на разстояние S'=40.25 от вдлъбнато-изпъкнал менискус. Параметри на лещата: d=10, радиуси: 100 и 15, n=1,5. Намерете позицията на елемента(ите).

В този случай веднага е необходимо да се справите със знаците на радиусите. R1=-100, R2=-15.

Параксиални характеристики на системата: f'=33.96; SF = -26,42; S'F= 35,09

Нека използваме формулата на Нютон за изчисления: f f'=z z'

Според формулата на Нютон z=f f'/z'=-223,58.

4.4. Определяне на параксиални параметри на концентрични лещи

Концентричните лещи са лещи, при които центровете на кривината на двете повърхности съвпадат. Следователно дебелината на лещата се изчислява по формулата:

При определяне на параксиалните параметри на концентричните лещи е характерно съвпадението на основните равнини в центъра на кривината на двете повърхности:

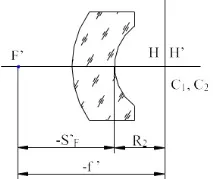
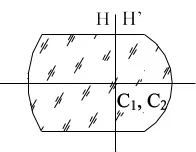
Фокусно разстояние на топката за близане f'=75 mm. Определете радиуса на топката, ако коефициентът на пречупване n=1,5.

Ф=2 (n-1)/(n r) определят фокусното разстояние на сферичната леща:

Следователно, радиус: r=f' 2 (n-1)/n

Отговор:Радиусът на сферичната леща е 50 mm.

5.1. Изчисляване на матрицата на Гаус на оптична система

Стойности на елементите на матрицата на Гаус за спрегнати равнини:

Aима значението на линейно увеличение.

За случая на конюгирана препраткаравнини елементB=0.

ЕлементътСне зависи от положението на опорните равнини и винаги е равен на оптичната сила с обратен знак.

ЕлементътDе реципрочната стойност на елементаAи за фокалната система има значението на ъглово увеличение:D=

Обект от 5 mm се поставя на 150 mm пред леща с изпъкнала равнина с радиус на повърхността 50 mm, дебелина 10 mm и индекс на пречупване 1,5. Определете размера и позицията на изображението спрямо последната повърхност S'. Решете задачата с помощта на матрици. Проверете решението.

Първо, необходимо е да се определят параксиалните характеристики на системата. Съгласно съотношенията, дадени в практическа работа 4, получаваме: f'=100; SH=0; S'H=-6,67.

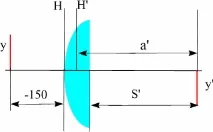
Ние съставяме матрицата на трансформация на лъчи от системата, чиито референтни равнини са разположени в равнините на обекта и изображението за тази задача. Очевидно ще има три трансформации, от обекта към основната равнина - трансферT0, върху главните равнини - пречупванеR1, към изображението - трансферT1.

И така матрици:

Матрица на цялата системаG=T1·R1·T0. Правилата за умножение на матрици могат да бъдат намерени в "Приложение P3. Аритметични операции върху матрици". Резултатът от матричното произведение ще ни даде матрица с едно неизвестно - a':

Условието за сдвояване на референтните равнини казва, че матричният елементB=0. Правим уравнението 150-0,5a'=0, така че a'=300.

Определяне на размера на изображението. Изображение y'=y β

Системното увеличение е равно на стойността на елементаA. β=1-3=-2.

---