Задачи за избор на маршрут или мрежови задачи 3

Транспортни задачи 3

Алгоритъм за решаване на транспортната задача 7

Пример за решаване на транспортна задача 7

Мрежови задачи 13

Алгоритъм за решаване на мрежов проблем 19

Намиране на минималния скелет в графика с пример за решаване на задача 19

Намиране на най-краткия път в графика с пример за решаване на задача 21

Примери за решаване на проблеми в Microsoft Office Excel 2003 и Mathcad 2001i Professional 24

Литература 32

Математиката е необходима в ежедневието, следователно, определени математически умения са необходими за всеки човек. Трябва да броим в живота, постоянно използваме знания за количествата, които характеризират степента, площта, обема, интервалите от време, скоростта и много други. Всичко това дойде при нас в уроците по аритметика и геометрия и беше полезно за ориентация в света около нас.

Математическите знания и умения са необходими в почти всички професии, разбира се, най-вече в тези, свързани с природните науки, технологиите и икономиката. Математиката е езикът на природните науки и технологиите и затова професията на естествения учен и инженер изисква сериозно владеене на много професионална информация, базирана на математиката.

Днес има несъмнена необходимост от прилагане на математически знания и математическо мислене към лекар, лингвист, историк и хора с други специалности. Но особено знанията по математика са необходими на хората с точни професии - финансисти, икономисти. Следователно математиката и математическото образование са необходими за подготовка за бъдеща професия.

Един от класовете математически модели са задачите на линейното програмиране. Един от проблемите на линейнатапрограмирането е транспортна задача - задачата за съставяне на оптимален транспортен план, който позволява минимизиране на общия пробег.

Целта на тази курсова работа по курса "Теория на информационните процеси и системи" е анализът на теоретичната част, получена в лекционния курс и самостоятелното прилагане на практика на теоретичните знания за решаване на проблеми при изучаването на системи.

В тази курсова работа ще направя изводи при разработването на оптимално решение за намиране на най-краткия път между няколко дадени точки, което би било най-високо ефективно.

Обект на изследването е транспортирането на стоки от точките на производство до точките на потребление, както и намиране на най-късото разстояние между точките в графиките.

Целта на работата: да се определи системата за оптимално управление на превоза на товари и да се намери най-краткият начин да се харчат по-малко пари.

Актуалността на темата се състои в това, че задачите за избор на маршрут са приложими навсякъде, но най-често те се срещат при изучаването на различни процеси в транспорта и в комуникационните системи (компютърни мрежи).

Задачи за избор на маршрут или мрежови задачи.

Типичен проблем за избор на маршрут е да се намери някакъв маршрут от един град до друг, дадени множество пътища през различни междинни точки. Проблемът е да се определи най-икономичният маршрут по отношение на време, разстояние или цена.

При разглеждане на редица маршрути се въвеждат следните ограничения:

- забранено е връщането към вече преминатата точка,

- възможни са забавяния в точките на мрежата (например поради ограничена честотна лента). Закъсненията са случайни.

Критерии за оптимизация: Минимизиране на общата суматранзитно време или минимизиране на общите разходи.

Един пример за такива проблеми е проблемът с пътуващия търговец.

Проблемът с пътуващия търговец е един от най-известните задачи за комбинаторна оптимизация. Задачата е да намерите най-печелившия маршрут, минаващ поне веднъж през посочените градове и след това връщане в първоначалния град. В условията на проблема са посочени критерият за рентабилност на маршрута (най-краткият, най-евтиният, кумулативен критерий и т.н.) и съответните матрици на разстояния, разходи и т.н.. Като правило е посочено, че маршрутът трябва да минава през всеки град само веднъж - в този случай изборът се прави между цикли на Хамилтон.

Има няколко специални случая на общата формулировка на проблема, по-специално геометричният проблем на търговския пътник (наричан още планарен или евклидов, когато матрицата на разстоянието отразява разстоянията между точките в равнината), проблемът на триъгълния търговец (когато неравенството на триъгълника е изпълнено върху матрицата на разходите), симетрични и асиметрични проблеми на търговския пътник. Съществува и обобщение на проблема, т. нар. обобщен проблем на продавача.

Общата постановка на задачата, обаче, както повечето частни случаи, принадлежи към класа на NP-трудните задачи.

По един или друг начин всичко се свежда до решаването на транспортния проблем.

Транспортната задача се разделя на два вида: транспортна задача според критерия цена - определяне на транспортен план, при който цената на товара би била минимална; транспортна задача по времевия критерий - по-важна е печалбата във времето.

Транспортната задача според критерия цена е частен случай на задачата за линейно програмиране и може да бъде решена чрез симплексния метод. Въпреки това, впоради особеностите на проблема се решава много по-лесно.

Този проблем се свежда до определяне на такъв план за транспортиране на даден продукт от точките на неговото производство до точките на потребление (║xi,j║mxn), който минимизира целевата функция

върху набора от изпълними планове

при условие на баланс

Транспортната задача е представител на класа задачи на линейното програмиране и следователно притежава всички качества на задачите за линейна оптимизация, но в същото време има редица допълнителни полезни свойства, които са направили възможно разработването на специални методи за нейното решаване.

Ако приведем условията на транспортния проблем до каноничната форма на проблема с линейното програмиране, тогава матрицата на проблема ще има размерност (m + n) x mn. Матриците на системите от уравнения в ограниченията (3.2) и (3.3) имат рангове, равни съответно на m и n. Ако обаче, от една страна, сумираме уравнения (3.2) върху m, а от друга страна, сумираме уравнения (3.3) върху n, тогава по силата на (3.5) получаваме същата стойност. От това следва, че едно от уравненията в системата (3.2)-(3.3) е линейна комбинация от останалите. По този начин рангът на матрицата на транспортния проблем е равен на m+n-1 и нейният неизроден базов дизайн трябва да съдържа m+n-1 ненулеви компоненти.

Удобно е процесът на решаване на транспортния проблем да се организира под формата на последователност от таблици, чиято структура е показана на фиг. 3.1.

Редовете на транспортната таблица съответстват на точките на производство (последната клетка на всеки ред съдържа обема на запасите на продукта ai), а колоните съответстват на точките на потребление (последната клетка на всяка колона съдържа стойността на търсенето bj). Всички клетки на таблицата (с изключение на тези, разположени в долния ред и дясната колона) съдържат информация за транспорта от i-та точка до j-та: в горния ляв ъгъле цената на транспортиране на единица продукт, а в долния десен ъгъл - стойността на обема превозен товар за тези точки. Клетките, които съдържат нулеви транспорти (хi, j = 0), се наричат свободни, а ненулевите транспорти се наричат заети (xi, j> 0).

По аналогия с други задачи на линейното програмиране, решаването на транспортната задача започва с изграждането на допустим базисен план. Най-лесният начин за намирането му се основава на така наречения метод на северозападния ъгъл. Същността на метода е последователното разпределение на всички запаси, налични в първи, втори и т.н. пунктове на производство, според първи, втори и т.н. пунктове на потребление. Всяка стъпка на дистрибуция се свежда до опит за пълно изчерпване на запасите в следващата точка на производство или до опит за пълно задоволяване на нуждите в следващата точка на потребление. На всяка стъпка q текущите неразпределени резерви се означават като ai(q), а текущите незадоволени нужди се означават с bj(q). Изграждането на приемлив първоначален план, според метода на северозападния ъгъл, започва от горния ляв ъгъл на транспортната маса, като приемаме ai(0) = ai, bj(0) = bj. За следващата клетка, намираща се в ред i и колона j, се вземат предвид стойностите на неразпределения запас в i-тата точка на производство и незадоволената потребност на j-тата точка на потребление, от тях се избира минимумът и се задава като обем на транспортиране между тези точки: xi,j = min. След това стойностите на неразпределения запас и незадоволеното търсене в съответните точки се намаляват с тази сума:

Очевидно на всяка стъпка е изпълнено поне едно от равенствата: ai(q+1)=0 или bj(q+1)=0. Ако първото е вярно, това означава, че целият запас на i-тата производствена точка е изчерпан инеобходимо е да преминете към разпределението на запаса в производствената точка i + 1, т.е. да преминете към следващата клетка надолу в колоната. Ако bj(q+1)=0, тогава необходимостта от j-тия елемент е напълно удовлетворена, след което следва преход към клетката, разположена вдясно от реда. Новоизбраната клетка става текуща и за нея се повтарят всички изброени операции.

Въз основа на условието за баланс на доставките и нуждите (3.5) е лесно да се докаже, че в краен брой стъпки ще получим допустим план. Поради същото условие, броят на стъпките на алгоритъма не може да бъде повече от m+n-1, така че винаги ще има свободни (нула) mn-(m+n-1) клетки. Следователно полученият план е основен. Възможно е на някаква междинна стъпка текущият неразпределен запас да се окаже равен на текущата незадоволена нужда (ai(q) = bj(q)). В този случай преходът към следващата клетка се извършва в диагонална посока (текущите точки на производство и потребление се променят едновременно), което означава „загуба“ на един ненулев компонент в плана или, с други думи, дегенерация на изградения план.

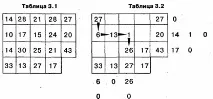
Помислете за прилагането на метода на северозападния ъгъл на конкретен пример. Транспортна таблица 3.1 съдържа условията на определена задача, а в табл. Фигура 3.2 показва процеса на намиране на приемлив план, включително последователна промяна в обема на неразпределените запаси и незадоволените нужди. Стрелките отразяват траекторията на преход през клетките на транспортната таблица, а числата извън нея са текущите неразпределени салда след присвояване на обема на следващата клетка.

Характеристика на допустимия план, конструиран по метода на северозападния ъгъл, е, че целевата функция върху него приема стойността, като правило,далеч от оптималното. Това се случва, защото стойностите на ci,j не се вземат предвид при конструирането му. В тази връзка на практика за получаване на първоначалния план се използва друг метод - методът на минималния елемент, при който при разпределяне на обемите на трафика първо се заемат клетки с най-ниски цени.

Алгоритъм за решаване на транспортната задача.

Задачата може да се реши с помощта на алгоритъма за решаване на транспортната задача. Прилагането на този алгоритъм изисква спазването на редица предпоставки:

1. Разходите за транспортиране на единица продукт от всяка точка на производство до всяка дестинация трябва да бъдат известни.

2. Трябва да се знае запасът от продукти във всяка точка на производство.

3. Изискванията към храните във всяка точка на консумация трябва да бъдат известни.

4. Общото предлагане трябва да е равно на общото търсене.

Алгоритъмът за решаване на транспортния проблем се състои от четири етапа:

Етап I. Представяне на данните под формата на стандартна таблица и търсене на приемливо разпределение на ресурсите. Приемливото разпределение на ресурсите е такова, че да задоволява цялото търсене в дестинациите и да премахва цялото предлагане на продукти от производствените точки.

Етап 2. Проверка на оптималността на полученото разпределение на ресурсите

Етап 3. Ако полученото разпределение на ресурсите не е оптимално, тогава ресурсите се преразпределят, намалявайки разходите за транспорт.

Етап 4. Повторна проверка на оптималността на полученото разпределение на ресурсите.

Този итеративен процес се повтаря, докато се получи оптимално решение.

Пример за решаване на транспортна задача.

Задача 1. От трите хладилника Ai, i=1..3, съдържащи замразена риба в количества ai t, ви трябва последниятдоставя до пет магазина Bj, j=1..5 в количества bj t.Разходите за транспортиране на 1 тон риба от хладилника Ai до магазина Bj са дадени като матрица Cij, 3x5.

Напишете математически модел на задачата и планирайте транспорта така, че общата им цена да е минимална.

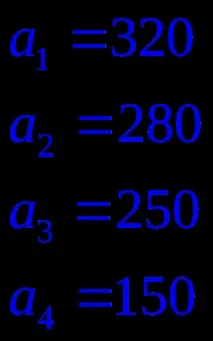
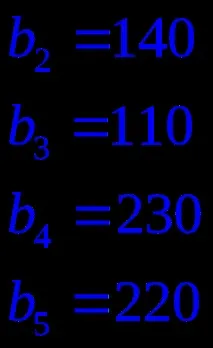
Нека направим математически модел на проблема. Нека xi,j е броят m риби, транспортирани от хладилника (доставчик) Ai до магазина (потребител) Bj. Тогава задачата е да се минимизират общите транспортни разходи

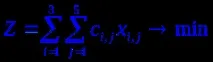
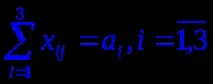
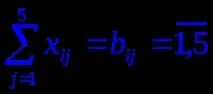
Задачата е от затворен тип, т.к товарни запаси 320+280+250 = 850 тона са равни на общите нужди на складовете 150+140+110+230+220 = 850 тона.

Ще съставим основен план по правилото на минималния елемент.

Задачи за избор на маршрут или мрежови задачи 3 - Документ - Страница