Задачи за обработка на дърво

PascalABC.NET е език за програмиране Pascal от следващо поколение, който включва класически Pascal, повечето функции на езика Delphi и редица собствени разширения. Той е реализиран на платформата Microsoft.NET и съдържа всички модерни езикови функции: класове, претоварване на оператори, интерфейси, обработка на изключения, генерични класове и подпрограми, събиране на отпадъци, ламбда изрази, инструменти за паралелно програмиране.
PascalABC.NET е многопарадигмен език: може да се използва за програмиране в структурен, обектно-ориентиран и функционален стил.
PascalABC.NET също е проста и мощна IntelliSense активирана IDE с инструменти за автоматично форматиране, вграден дебъгер и вграден дизайнер на формуляри.
Книга: Описание на езика PascalABC.NET
Задачи за обработка на дърво
Секции на тази страница:
Задачи за обработка на дърво
Пример 1. Анализ на двоично дърво
В задачите от групата Tree, както и в задачите от групата Dynamic, срещаме два нови типа данни: това садървовидни динамични структури, реализирани като набори от записи тип TNode, свързани помежду си, иуказателиот тип PNode към записи на TNode: PNode = ^TNode. Типовете TNode и PNode не са стандартни типове Pascal; те са определени в учебника по програмиране.
Ще разгледаме функциите, свързани с използването на нови типове данни, използвайки задачата Tree2 като пример.
Създаване на програма за пънове и запознаване със задачата
Спомнете си, че празна програма за решаване на тази задача може да бъде създадена с помощта на командата от менюто Модули Създаване на шаблон на програма", бутони
използва PT4;начало Задача('Дърво2');край.
След стартиране на програмата на екрана ще се появи прозорец със задачи:
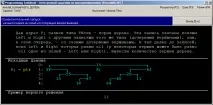
Този прозорец съдържа нови елементи като входни и изходни данни: двоични дървета и указатели.
Нека започнем, като опишем какдървотосе показва на екрана. Той използва няколко реда на екрана, за да го покаже. Всеки ред показва върховете на дървото, които са на определено ниво (номерът на нивото е посочен отляво на изображението на дървото). За всеки връх се показва неговата стойност, т.е. стойността на полето Data на съответния запис от типа TNode. Всеки връх е свързан с линии със своите дъщерни върхове, разположени на следващото ниво на дървото; левият дъщерен връх е начертан отляво на родителския връх, а десният дъщерен връх е начертан отдясно. Ако даден възел има един или двата дъщерни възела, тогава полетата му Ляво и/или Дясно са нула.
Разгледайте дървото, показано на фигурата, като пример. Коренът на това дърво е 15, лявото дете на корена е 58, дясното дете е 42, а дълбочината на дървото е 4. Всички листа на дървото са на нива 3 и 4; листата на ниво 3 имат стойности 15 и 11, листата на ниво 4 имат стойности 38 и 84. Някои от вътрешните възли на дървото имат по две деца (това са коренът и възлите със стойности 55 и 20), някои имат едно: ляво (възли 42, 87 и 60) или дясно (възел 58).
Работата с данни от тип указател източник и резултат е разгледана подробно в раздела за линейни динамични структури.
Решението на проблема
Работата Tree2 не изисква да създавате или трансформирате оригиналното дърво; необходимо е само да се анализира, а именно да се определи броят на неговите върхове.
За да изпълните тази задача, както и за огромното мнозинствоповечето други задачи за обработка на дърво, трябва да използвате помощнарекурсивнаподпрограма (функция или процедура). Рекурсивният характер на алгоритмите, свързани с обработката на дървета (по-специално на двоични дървета), се обяснява с факта, че дефинициите на общите дървета и самите двоични дървета са рекурсивни. По този начин, за да се даде словесно описание на функцията NodeCount(P), която брои броя на върховете на дървото с корена, свързан с указателя P, може да бъде както следва: ако указателят P е равен на нула, тогава трябва да се върне стойността 0; в противен случай върнете 1 + NodeCount(P^.Left) + NodeCount(P^.Right) (в този израз първият член съответства на корена на дървото, вторият на неговото ляво поддърво, а третият на неговото дясно поддърво; няма нужда да проверявате дали посочените поддървета съществуват, тъй като ако те не съществуват, съответният член просто ще бъде нула).
Така решението на проблема ще изглежда така:
използва PT4;функция NodeCount(P: PNode): цяло число; започнетеако P = нулатогава резултат := 0друго резултат := 1 + NodeCount(P^.Left) + NodeCount(P^.Right);край ;вар. P1: PNode;начало Задача('Дърво2'); четене (P1); запиши(NodeCount(P1));край.
Ако изпълним тази програма пет пъти, ще получим съобщението Job Complete!".
Пример 2. Двоични дървета с обратна връзка
Дървета, чиито върхове съдържат информация за своите родители, ще се наричат дървета за обратна връзка. Ще разгледаме характеристиките на работата с такива дървета, като използваме задачата Tree49 като пример.
Дърво49°. Даден е указателP1 към корена на дървото, чиито върхове са записи от тип TNode, свързани междусебе си, като използвате полетата Ляво и Дясно. Използвайки полето Parent на записа TNode, преобразувайте дървото източник вдърво за обратна връзка, в което всеки възел е свързан не само със своите дъщерни възли (полетата Left и Right), но и с възела родител (полето Parent). Задайте полето Родител на корена на дървото на нула.
Като стартираме програмата за заглушаване, създадена за задачата Tree49, ще видим в областта на изходните данни изображение на обикновено "двоично дърво", докато в областта на резултатите ще видим дърво с обратна връзка, чиито върхове са свързани не с единични, а с двойни линии.
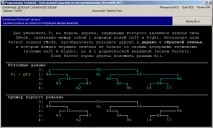
За да преобразувате изходно дърво в дърво с обратна връзка, трябва да зададете правилните стойности за родителските полета на всички възли в дървото, като итерирате тези възли с помощта на подходяща рекурсивна процедура. Удобно е да се предаде като параметри на тази процедура не само указателят P към текущия връх, но и указателят Par към предшественика на този връх:
използва PT4;процедура SetParent(P, Par: PNode);започнетеако P = нулатогава излезте; P^.Parent := Par; SetParent(P^.Left, P); SetParent(P^.Right, P);край ;вар. P1: PNode;начало Задача('Дърво49'); четене (P1); SetParent(P1, нула);край.
При стартиране на рекурсивната процедура SetParent, nil се посочва като втори параметър.
Забележка. Нотацията за двойната връзка може да бъде полезна при анализиране на грешното решение. Така че, ако в изображението на дърво с обратна връзка има връх, свързан с неговия родителски връх не с двойна, а с една линия, тогава полето Parent на този връх съдържа грешна стойност (например, то е равно на нула).
Пример 3. Генерични дървета
С помощта на свързани записи от типа TNode е възможно да се моделират не само двоични дървета, но и произволно подредени дървета, чиито върхове имат произволен брой непосредствени деца (ще наричаме такива дърветаобщи дървета; те се наричат също многоразклонени дървета").
Дърво86°.Генерично дърво(всеки връх от което може да има произволен брой дъщерни върхове, подредени във фиксиран ред отляво надясно) се реализира с помощта на набор от свързани записи от тип TNode, както следва: за всеки вътрешен връх лявото му поле съдържа указател към неговия първи (т.е. ляв) дъщерен връх, а дясното поле съдържа указател към неговата дяснасестра, т.е. tex, който има същия родител в общото дърво. Дясното поле на общ корен на дърво винаги е нула, тъй като коренът няма сестри. Даден е указателP1 към корена на непразно двоично дърво. Създайте общо дърво, съответстващо на оригиналното двоично дърво и изведете указателяP2 към неговия корен.
Ето пример за дърво с общ изглед, което се реализира с помощта на свързани записи от типа TNode (по подобен начин дърветата с общ изглед се показват в прозореца на книгата със задачи):
Коренът на това дърво (със стойност 13) има три деца (71, 73 и 29), като възел 71 няма деца, възел 73 има три непосредствени деца (18, 93 и 92), а възел 29 има две (24 и 84). Последното ниво съдържа възел 46, който е единственото дете на възел 93.
Когато стартирате Tree86 Job Trial, ще видите екран, подобен на следния.
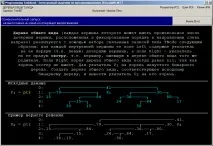
Обърнете внимание как изглежда едно и също дърво в две различни представяния: вариантът, съответстващ на обикновеното двоично дърво, е даден в секцията с изходни данни, а вариантът, съответстващ на общото дърво, е даден в секцията с резултати. При преминаване от двоично дърво към общо дърво се губи част от информацията за структурата на двоичното дърво, тъй като ако някой възел от общото дърво има само едно непосредствено дете, е невъзможно да се определи дали това дете е било в оригиналното двоично дърво - ляво или дясно.
Спомнете си, че точките, рамкиращи стойностите на върховете в секцията с резултати, означават, че всички тези върхове трябва да бъдат създадени от програмата на ученика (за разлика от върховете на изходното дърво, създадено от самата книга с проблеми, когато задачата е инициализирана).
използва PT4;функция CreateNode(P: PNode): PNode;вар. P1, P2: PNode;започнетеако P = нулатогавазапочнете резултат := нула; изход;край ; Нов (резултат); result^.Data := P^.Data; result^.Right := нула; P1 := P^.Left; P2 := P^.Right;ако P1 = нулатогавазапочнете P1 := P2; P2 := нула;край ;резултат^.Наляво := CreateNode(P1);ако P1 <> нуласлед това резултат^.Наляво^.Надясно := CreateNode(P2);край ;вар. P1: PNode;започнете Задача('Tree86'); четене (P1); запис (Създаване на възел (P1)); край.