Заварени, нитовани, резбови съединения на машинни части - Момент на завинтване, ефективност и състояние
Машинни части: заварени, нитовани, резбови съединения - Момент на завинтване, ефективност и състояние на самоспиране
Момент на затягане, ефективности състояние на самоспиране
Връзки между сили и въртящ моментв резбова връзка. Първо ще проучим зависимостите за правоъгълни резби и след това ще ги разширим към други видове резби.
При отчитане на силите в двойка винтове е удобно да завъртите резбата по протежение на средния диаметър d2 в наклонена равнина и да замените гайката с плъзгач (фиг. 4.22, а). Силата на взаимодействие на наклонената равнина с плъзгача по време на относително движение е резултат от нормалната сила и силата на триене. Следователно тази сила е наклонена към нормалното n под ъгъл на триене φ. В резултат на разширяването на силата получаваме
, (4.2)
където Ft е задвижващата периферна сила; F - аксиална сила върху винта; е ъгълът на спиралата на нишката.
Периферентната сила на триене в триъгълна резба е по-голяма, отколкото в правоъгълна резба. Удобно е да се вземе предвид съотношението на периферните сили на триене в правоъгълни и триъгълни нишки на модели с пръстеновидни завои, като се приеме, че ъгълът на резбата е равен на нула (Фигура 4.22, b).
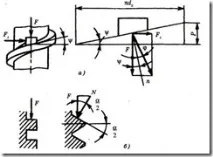
Фигура 4.22 - Сили на взаимодействие между винта и гайката
Периферна сила на триене за намотка с правоъгълен профил За намотка с триъгълен профил F1=Nf
За бобина с триъгълен профил
, (4.3)
Където ; е ъгълът на профила на резбата, от който намаленият коефициент на триене
. (4.4)
По този начин силата на триене в триъгълна нишка може да се определи по същия начин, както в правоъгълна, само че вместо действителния коефициент на триене трябва да се използва намаленият, равен на реалния, разделен нана cos(a/2).
Подобна зависимост има и между ъглите на триене:
. (4,5)
За нормална метрична резба ъгълът (ss / 2) \u003d 30 ° и следователно,
f1 ≈ 1,15
u = 1,15 (тук е намаленият ъгъл на триене).
За да определите задвижващата периферна сила в триъгълна резба, можете да използвате получената формула за правоъгълна резба, като заместите намаления ъгъл на триене вместо действителния.
Въртящ момент на гайката или винта с капачка
където Tr е моментът в резбата; TT е моментът на триене в края на гайката или главата на винта. Въртящ момент на резбата
. (4,7)
Носещата повърхност на гайката и главата се приема като пръстеновидна с външен диаметър, равен на гаечния ключ D1 и вътрешен диаметър, равен на диаметъра на отвора на винта d0.
Въртящ момент на триене в края на гайка или глава
, (4.8)
Където ; е коефициентът на триене в края на гайката.
Тази лесна за изчисляване зависимост се основава на предположението, че налягането при повърхността на гайката се увеличава с намаляване на радиуса. Увеличаването на налягането е свързано с еластична деформация на тялото на гайката и намалени пътища на триене при малки радиуси по време на завинтване и развиване.
Въртящият момент в края на гайката или главата на винта е около 50% от общия момент на затягане.
Замествайки получените изрази Tr и Tm във формулата за момента на завинтване, накрая получаваме
. (4,9)
При развиване на гайката периферната сила Ft и силите на триене променят посоката си в обратна посока. В този случай получаваме Ft = Ftg().
Моментът на развиване, като се вземе предвид триенето в края на гайката, по аналогия с момента на завинтване ще има формата
. (4.10)
Получените зависимости ни позволяват да отбележим:
Използвайки формула (4.9), можем да изчислим съотношението на аксиалната сила на винта F към силата F, приложена върхудръжката на ключа, което дава печалба в силата. За стандартни метрични резби със стандартна дължина на ключа
и \u003d 0,15 \u003d 70 - 80.
Винтовият вал не само се разтяга от силата F, но и се усуква от момента Tr.
Условието на самоспиране може да се запише като Тotv > 0, където Тotv се определя по формулата (4.10). Разглеждайки самоспирането само в резбата, без да отчитаме триенето в края на гайката, получаваме tg( ) > 0 или