1. Обемът на цилиндрично тяло. Двоен интеграл.

Приложение на двойни интеграли към задачи на механиката и геометрията.

катедри по висша математика

2. Изчисляване на двойни интеграли.

3. Приложения на двойните интеграли към проблемите на механиката.

а) масата на плоска плоча с променлива плътност.

б) статични моменти и център на тежестта на плочата.

в) инерционни моменти на плочата.

4. Изчисляване на площи и обеми чрез двойни интеграли.

б) Изчисляване на площта на плоска площ.

5. Изчисляване на повърхността.

1. Обемът на цилиндрично тяло. Двоен интеграл.

Цилиндрично тяло е тяло, ограничено от равнината Oxy, повърхност, с която всяка линия, успоредна на оста Oz, се пресича в не повече от една точка, и цилиндрична повърхност, чиято образуваща е успоредна на оста Oz.

Областта D, изрязана в равнината Oxy от цилиндрична повърхност, се нарича основа на цилиндричното тяло (виж фиг. 1). В специални случаи страничната цилиндрична повърхност може да отсъства; пример за това е тяло, ограничено от равнината Oxy и горното полукълбо.

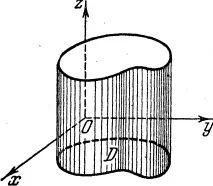
Обикновено едно тяло може да бъде съставено от определен брой цилиндрични тела и желаният обект може да се определи като сбор от обемите на цилиндричните тела, които изграждат това тяло.

На първо място, припомняме два принципа, от които изхождаме, когато определяме обема на тялото:

ако разбиете тялото на части, тогава неговият обем ще бъде равен на сумата от обемите на всички части;

обем на прав цилиндър, т.е. на цилиндрично тяло, ограничено от равнина, успоредна на равнината Oxy, е равна на площта на основата, умножена по височината на тялото.

Нека има уравнение на повърхността, ограничаваща цилиндричното тяло. Ще приемем, че функцията е непрекъсната в регионаD и първо приемете, че повърхността лежи изцяло над равнината Oxy, т.е. което е навсякъде в D.

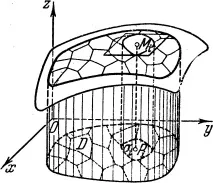
Нека обозначим желания обем на цилиндричното тяло чрезV,Нека разделим основата на цилиндричното тяло - област D - на определен брой n области с произволна форма; ще ги наречем частични региони. След като номерираме частичните региони в някакъв ред, ние ги означаваме с, а техните площи - с. Нека начертаем цилиндрична повърхност през границата на всяка частична област с образуваща, успоредна на оста Oz. Тези цилиндрични повърхности ще разрежат повърхността на n части, съответстващи на n частични области. Така цилиндричното тяло ще бъде разделено на n частични цилиндрични тела (виж фиг. 2). Избираме произволна точка във всяка частична област и заместваме съответното частично цилиндрично тяло с прав цилиндър със същата основа и височина, равна на. В резултат на това получаваме n-стъпково тяло, чийто обем е равен на

Вземайки обемаVна това цилиндрично тяло, приблизително равен на обема на конструираното n-стъпково тяло, ще приемем, че Vn изразяваV,колкото по-точно е по-голямото n и по-малката всяка от частичните области. Преминавайки към границата при ще изискваме не само площта на всяка частична област да клони към нула, но и всички нейни измерения да клонят към нула. Ако наречемдиаметър на областнай-голямото разстояние между точките на нейната граница (Например диаметърът на правоъгълник е равен на неговия диагонал, диаметърът на елипса е неговата главна ос. За кръг горната дефиниция на диаметър е еквивалентна на обичайната.), тогава заявеното изискване ще означава, че всеки от диаметрите на частични области трябва да клони към нула; в този случай самите региони ще се свият до точка (ако е известно само, че площта на региона има тенденция данула, тогава този регион може да не се свие до точка. Например площта на правоъгълник с постоянна основа и височина, клоняща към нула, клони към нула, а правоъгълникът се свива до основата си, т.е. до сегмент).

В съответствие с горното, ние приемаме желания обемVравен на границата, към която Vn клони, когато най-големият диаметър на частичните области клони към нула (в този случай):

Голямо разнообразие от проблеми води до намиране на границата на подобни суми за функции на две променливи, а не само проблемът с обема.

Нека разгледаме този въпрос по общ начин. Нека - всяка функция на две променливи (не непременно положителни), непрекъсната в някаква област D,, ограничена от затворена линия. Нека разделим областта D на частични, както е посочено по-горе, изберете произволна точка във всяка частична област и съставете сумата

(*)

където е стойността на функцията в точката; и е площта на частичния регион.

Сумата (*) се нарича n-та интегрална сумаза функцията в областта D,, съответстваща на даденото разделяне на тази област на n частични области.

Определение.Двойният интеграл на функция върху областта D е границата, към която n-тата интегрална сума (*) клони, когато най-големият диаметър на частичните области клони към нула.

Написано е така:

Той гласи: „двоен интеграл от напо област D“. Израз, показващ формата на сумирани членове, се нарича интегранд; функцията се нарича интегранд, елементът на областта, областта D е областта на интегриране и накрая, променливите x и y се наричат променливи на интеграция.

По този начин можем да кажем, че обемът на цилиндрично тяло, ограничено от равнината Oxy,и цилиндричнатаповърхност с образуваща, успоредна на оста Oz,се изразява чрез двоен интеграл на функцията,, взета върху площта, която е основата на цилиндричното тяло:

Подобно на теоремата за съществуване на обикновен интеграл, важи следната теорема.

Теорема за съществуване на двоен интеграл.

Ако дадена функция е непрекъсната в област D, ограничена от затворена линия, тогава нейната n-та интегрална сума клони към границата, тъй като най-големият диаметър на частичните области клони към нула. Тази граница, т.е. двоен интеграл не зависи от метода на разделяне на област D на частични области и от избора на точки Piв тях.

Двойният интеграл, разбира се, е число, което зависи само от интегранта и областта на интегриране и изобщо не зависи от записа на интеграционните променливи, така че, например,

След това ще видим, че изчисляването на двойния интеграл може да се направи с помощта на две обикновени интеграции.