10 тайни тригонометрични функции, които никога не са ви учили на математика
Математика за ученици и студенти, обучение и възпитание
10 тайни тригонометрични функции, за които никога не са ви учили
Има 10 тайни тригонометрични функции, за които никога не сте чували, и те имат невероятни имена като хаверсинус и изпълнение.
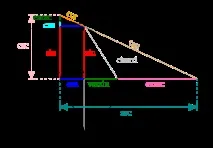
Ориз. 1. Тук е единичната окръжност и повече от изобилие от тригонометрични функции. (Известни са максимум 8 тригонометрични функции). Познатите синус, косинус и тангенс са маркирани съответно в синьо, червено и жълтокафяво. Версинусът е маркиран в зелено до косинуса и розовият екзекант вдясно от версинуса. Екскосекант и синус коверсус също са показани на фигурата. Vercosine, cosine-coversus и всичко от Gaver не са посочени.
Ако искате да измъчите учениците с това и да завъртите интересни думи в разговор, за да звучи ерудирано и/или непоносимо, ето дефинициите на всички „забравени тригонометрични функции“:
версинус: , веркосинус: , синус-коверсус: , косинус-коверсус: , хаверсинус: , хаверсинус: ; когаверсин: , когаверсин: , изпълнение: , еккосеканс: .
Трябва да признаете, че изпитвате известно разочарование, когато видите това. Тези функции са прости комбинации от добрия стар синус и косинус. Защо са получили собствени имена?! За това време и място, където мога да намеря синуса на произволен ъгъл до 100 знака след десетичната запетая почти мигновено с помощта на онлайн калкулатор, седнал на дивана, версинът не е необходим. Но тези привидно излишни функции бяха необходими в света преди калкулатора.
В мрачните дни преди калкулатора хората са използвали логаритми за умножаване на големи числа. Първо, нека си спомним какво елогаритми. Равенството означава, че. Например, , така че . Използването на логаритми е удобно, защото. С други думи, логаритмите превръщат умножението в събиране. Ако искате да умножите две числа с помощта на логаритмична таблица, ще намерите логаритмите на двете числа в нея и след това ще ги съберете. След това в таблицата с логаритми ще намерите числото, което има полученият логаритъм и това ще бъде отговорът. Сега изглежда тромаво, но ръчното умножение изисква много повече операции. Когато всяка операция отнема определено време (и създава известна грешка), процедура, която преобразува умножението в събиране, спестява време и може да помогне за повишаване на точността на изчислението.
Тайни тригонометрични функции, като логаритми, опростени изчисления. Versinus и haversinus са използвани най-често. Ако ъгълът е близо до нула, неговият косинус е много близък до . Ако има в изчислението, тогава отговорът може да е грешен, ако вашата косинусова таблица няма достатъчно значими цифри. Например косинусът е , и . Разлика . Ако имате три значещи цифри във вашата косинусова таблица, ще получите само една значима цифра в резултата си поради нулите в разликата. А таблица само с три значещи цифри няма да покаже разликата между ъгли и . В много случаи това няма значение, но може да бъде проблем, ако възникне грешка по време на изчислението.
Допълнителните тригонометрични функции също имат предимството, че винаги са неотрицателни. Versine приема стойности от до , така че ако използвате логаритмична таблица с versin за умножение, не е нужно да се притеснявате, че отрицателните числа нямат логаритъм. (Не е дефинирано за нито едно от двете, но този случай е лесен за справяне). Друго предимство на versinus и haversinus е, че могатпремахване на необходимостта от квадрат. Малко тригонометрична мъдрост (като запаметяване на една тригонометрична формула от безкрайния списък с тригонометрични формули, които сте научили в училище) показва, че . По този начин хаверсин е просто . По същия начин хаверкосинусът е . Ако имате синус или косинус квадрат във вашите изчисления, можете да използвате таблиците за хаверсинус или хаверсинус и не е нужно да повдигате на квадрат или да вадите квадратен корен.
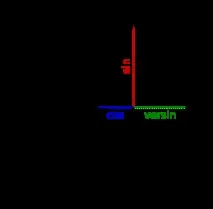
Ориз. 2. Фигурата показва синуса, косинуса и версинуса на ъгъл.
Има по-малко информация за историята на други тригонометрични функции от горния списък. Те помогнаха да се направят изчисленията по-точни в близост до определени ъгли, но някои от тях бяха широко използвани, докато други бяха кръстени на тях, но рядко се използваха. Може би някои от вас знаят повече за това. Пишете.
В таблицата на тайните тригонометрични функции „ха“ очевидно означава половина (от английската дума half), например хаверсинът е половината от версин. „Co“ означава същите функции, но от допълнителен ъгъл. (Допълнителен ъгъл е ъгъл, който се събира към даден ъгъл. В правоъгълен триъгълник два остри ъгъла са взаимно допълващи се.) Например косинусът на ъгъл е синусът на допълнителния ъгъл. По подобен начин синусът на коверсуса е версинът на допълнителния ъгъл. Посочено е в светло синьо над един от червените синуси на фиг. 1.
Това е просто малко объркващ веркосинус. Ако "co" означава допълнителен ъгъл, тогава веркосинусът ще бъде същият като корицинуса, което не е така. Вместо това веркосинусът е веркосинусът на съседния ъгъл (сумата от съседните ъгли е ), а не допълнителният. В допълнение към дефинициите по отношение както на versinus, така и на vercosine могат да бъдат определени катоИ . В случай на версинус, може би определението, включващо квадратния синус, е по-старо от определението, включващо квадратния синус. Може би някои от вас знаят повече за това.
Във всеки случай, таблицата със свръхсекретни допълнителни тригонометрични функции е забавно упражнение за намиране на значението на префиксите.