11 Letnija conferencija Turnira Gorodov
К. П. Кохас
0.1.Черните и белите епископи се поставят независимо по еднакъв брой начини - нека го обозначим с k . За всеки от k начина за поставяне на черни епископи има k начина за поставяне на бели епископи, така че общият брой начини е k 2 .
0,2.Броят начини за поставяне на един топ е площта на дъската.
0,4.Три топа на дъска 3*3 могат да бъдат поставени 3! начини. За да поставите три топа на дъска 8x8, е достатъчно първо да изберете три файла и три реда - това може да стане (C 3 8) по 2 начина, а след това върху получената дъска 3x3 вземете една от шестте подредби. Отговор: 6. 7 2 . 8 2 .
0,5.Упражнение за включване-изключване. Четири топа на цялата дъска могат да бъдат поставени 4!(C4 8) по 2 начина. Ако един топ е на диагонала, а останалите са произволни (стига да не се атакуват един друг), тогава има 8*3!*(C3 7) 2 такива подредби (първият фактор е броят начини за избор на едно място по диагонала, останалите са броят на подредбите на небиещи топове на дъската 7*7). Два топа по диагонала, а останалите могат да бъдат поставени произволноC2 8*2!*(C2 6) по 2 начина; три топа по диагонала, четвъртият, където иска, може да застанеC3 8*1!*(C1 5) по 2 начина; накрая, четири топа по диагонала могат да бъдат поставениC4 по 8 начина. Желаният брой начини е равен на променливата сума от преброените изрази
Наистина, в тази сума интересните за нас подредби се вземат предвид в първия израз и всички допълнителни подредби се вземат предвид в няколко израза с общ коефициент 0. Например подредбите с точно три топа по диагонала се вземат предвид веднъж в първия член, три пъти във втория, три пъти в третия и веднъж в четвъртия, като се вземат предвидзнаци, получаваме, че всички тези подредби са "намалени". Отговор: 70070.
1.1.Ако трябва да поставимnтопове и решим да поставимkот тях вC1, а останалите вC2, тогава имаrk(C1)rn-k(C2) такива договорености. означава,
1.2.Очевидно е. Помислете за разположението наnтопове. Ако не е поставен топ на полетоc, тогава топовете се поставят на дъскатаC1 и могат да бъдат поставени поrn(C1) начини. Ако топ е поставен на полетоc, тогава останалите (n-1) топове се поставят на дъскатаC2 и имаrn-1(C2) такива подредби. Така чеrn(C)=rn(C1)+rn-1(C2). Същото означава връзката с полиномите.
1.3.Например такава дъска (в горния ред от 2002 клетки): Друг пример: диаграма на Young с редове 1, 3, 5, 12, 41.
1.4.Автор на задачата е С. Волченков, задачата е използвана на 2-ра купа. Колмогоров. Въпросът на задачата е еквивалентен на следния въпрос:
На дъскатаn*nимаnнеатакуващи топове. Позволено е да питате за всяка клетка дали има топ или не. Какъв е минималният брой въпроси, които могат да се използват, за да се знае цялата подредба?
Отговор:n(n-1)/2. Например, можете първо да разберете къде се намира топът, разположен в първата колона. Това ще изисква не повече от (n-1) въпроса. Тогава откриваме къде точно се намира топът от втората колона. Това ще изисква не повече от (n-2) въпроса и т.н.
Нека докажем, че по-малко въпроси не са достатъчни. Да предположим, че някой се опитва да отгатне подредбата, като задава най-малко въпроси. Изневяра: няма да го направимпървоначално поставете топове на дъската и ние ще отговаряме с „не“ на всички въпроси на познатия, доколкото е възможно, като изрязваме квадратчетата, споменати във въпросите от дъската и се уверяваме, че е възможно да поставитеnтопове, които не се атакуват един друг върху останалите квадратчета. Обърнете внимание, че ще трябва да отговорим с "да" на въпроса на познатия за следващото полеCсамо ако за всички възможни подредби на небиещи топове на "отсечената" дъска трябва да има топ на полеC. Но в тази ситуация, дори и без въпроси, е ясно, че има топ на проверкатаC, така че с действията на познатия, които изискват най-малко въпроси, никога няма да трябва да отговаряме с "да".
Познаващият трябва да спре да задава въпроси в момента, когато на съкратената дъска ще съществува само една подредбаnот топове, които не се атакуват един друг. Без загуба на общоприетост можем да предположим, че това е единственото разположение наnтопове - по диагонал. След това за всяка двойка клетки, симетрични по отношение на този диагонал, познатият трябваше да зададе въпрос за поне една от клетките на тази двойка. Наистина, иначе поставяйки топове на тези полета (и премахвайки два подходящи топа от диагонала), получаваме ново подреждане на топове, което не противоречи на никой от горните отговори. Но след това изрязваме понеn(n-1)/2 клетки от дъската.
1.5.В една посока, това твърдение е очевидно: ако дъската се съдържа в обединението наkлинии, тогава, тъй като може да има най-много един топ на всяка линия, не може да има повече отkтопове общо (така да се каже, принципът на Дирихле с може би-може би-пресичащи се клетки).
От друга страна не е лесно. Преразказваме доказателството от [8].
Минималният брой редове, в обединението на коитопоставена е дъскаD, означетеm(D). НекаCm(C)=nза оригиналната платка. Ще премахваме клетки от дъскатаCколкото е възможно по-дълго, така чеmда не се променя. Получената дъска ще бъде означена сC1. Нека докажем, че топовете, поставени на всички клетки на дъскатаC1, няма да се атакуват един друг. Това ще установи, чеnнебиещи топове могат да бъдат поставени на оригиналната дъска.
Да предположим, че това не е така и клеткитеxиyна дъскатаC1 са на един и същи редl. Тъй като платкаC1 е минимална, следва, че платкаC1\xсе съдържа в обединението на семейство линииSx, състоящо се от (n-1) линии, а платкаC1\yсе съдържа в обединението на семейство линииSy, също се състои изписване на (n<9)>-1) линии иlPSx,lPSy.
НекаSе множеството от прави, включени само в едно от семействатаSx,Sy(т.е. симетричната разлика на множестватаSxиSy). Ако пресечната точка наSxиSyнабори се състои от m линии, тогаваSсе състои от 2(n-1- m) линии. Нека построим дъскаC2, състояща се от всички клетки на дъскатаC1, лежащи на пресечните точки на линии отSUl. Очевидноx,yCC2 и всяка клетка от дъскатаC1, която не лежи в обединението на линии отSx3Syпринадлежи наC2. КомплектътSUlсе състои от 2(n-1- m )+1 линии, така че дъскатаC2 може да бъде покрита от семействотоT, състоящо се от (n-1- m) линии (за това се отнасяме къмTсамо хоризонтални или само вертикални линии отSUl). И тогава цялата дъскаC1 е покрита от семейството линииTU(Sx3Sy). Но това семейство се състои от най-много (n-1- m + m) линии, което противоречи на дефиницията на дъскаC1. Полученото противоречие показва, че никакви две клетки от дъскатаC1 не могат да лежат на една и съща линия.
Отбелязваме като следствие следното преформулиране на този проблем:
За всяка дъска можете да задраскате хоризонтален или вертикален ред клетки по такъв начин, че степента на полинома на топа да намалява с единица.
2.2.Еквивалентните дъски имат еднакви зони, но сред всички диаграми с площn(n-1)/2Tnе единствената, на която има подреждане наn-1 непобеждаващи топа.
2.3.Изложението на проблема лесно се извежда от теоремата на Каплански или задача 6.2., но ние ще дадем пряко, почти биективно доказателство, следвайки [7]. Означаваме квадратаn*nсKn.
Нека докажем по индукция твърдението на проблема. Нека разделим квадратаKnна две части: квадратаKn-1 и "рамката", състояща се от 2n-1 клетки. Триъгълната дъскаYnсъщо ще бъде разделена на две части: дъскатаYn-1 и най-дългата хоризонтална (също от 2n-1 клетки). Да приемем, че съвпадението на номерата на топовете на полетоKn-1 и триъгълникаYn-1 вече е установено. Then we can assume that a correspondence has been built between the rook placements in then*nsquare, in which all the rooks are in the distinguished part (n-1)*(n-1), and the rook placements inYn, in which all the rooks are in the distinguished partYn-1. Остава да се изгради съответствие между разположенията на топовете вYn, които съдържат топа на дългия ред, и разположенията на топовете вKn, които съдържат топовете в "рамката". Обмисливсичкиkразположения на топове вYn, съдържащи топ в дълга линия, за които (k-1) разположението на топове вYn-1 е фиксирано, нека го наречемs, и съответното разположение вKn-1 -t. Общо има 2n-k=n+(n-k) такива подредби, тъй като има точно толкова полета, подходящи за последния топ в дълъг низ. Нека номерираме по някакъв начин тези клетки (фиг. 1).
Ако топът е на клетка с номерl, 1n(имаn-kтакива числа), тогава прилагаме подредбатаtв стандартното полеKn-1. Обърнете внимание, че сред (n-1) "рамкови" клетки, разположени надKn-1, има точно (n-k) места, където може да се постави топ. Е, нека поставим топа на (l-n)-то от тези места (фиг. 3).
Изградената кореспонденция е едно към едно.
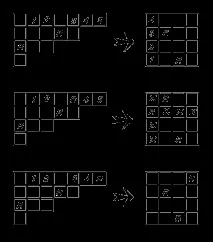
2.4.Означете оригиналните еквивалентни дъскиAиB, некаA' иB' са техните допълнения в правоъгълникаm*n,Rp,q(x) - топ полином на правоъгълникp*q. Използвайки принципа на включване-изключване, подобно на задача 0.2., е лесно да се изведе връзката