3. МЕТОД НА ДОКАЗВАНЕ (ДЕМОНСТРАЦИЯ)
3. МЕТОД НА ДОКАЗВАНЕ (ДЕМОНСТРАЦИЯ)
Разгледахме два компонента на доказателството: доказаната теза и основите на доказателството. Видяхме, че основната задача на едно доказателство е да направи безспорна или истинността на това, което се доказва, или неистинността на това, което се опровергава. Видяхме също, че истинността на една теза, която се доказва, или неистинността на една теза, която се опровергава, не може да бъде открита директно. За да се убедим в истинността на доказваната теза, трябва да посочим истинската основа, признавайки която за вярна, ние задължително трябва да признаем доказаната теза за вярна.
Но въпреки че е необходимо посочване на истинските основания за изясняване истинността на доказваната теза, само с това все още не постигаме целта на доказването. Само в отделни случаи посочването на истинското основание дава истинността на тезата, която се доказва веднага, под формата на пряк извод. Така че, ако се изисква да се докаже, че някои от равните един на друг ъгли са прави ъгли, тогава за да се докаже истинността на това твърдение е достатъчно да се позове като основа на истината, че всички прави ъгли са равни един на друг. От тази основа веднага, директно, само по законите на логиката (а именно по правилата на обръщението), се получава верен извод, че някои от равните един на друг ъгли са прави.
Но в по-голямата част от случаите познаването на истинските основания, водещи до признаването на истинността на тезата, не е достатъчно. Освен това е необходимо да се покаже каква е връзката, която задължително води от истинността на дадените основания към истинността на обусловената от тях теза. Тази връзка в много случаи не е пряко видима и изисква изясняване. По този начин, ако ученикът знае всички дефиниции, всички аксиоми и всички теореми, от истинността на които, както от основите, се извежда истината на Питагоровата теорема, товане означава, че ученикът знае доказателството на Питагоровата теорема. За да се знае доказателството, се изисква ученикът да знае каква е връзката между всички познати му основи на Питагоровата теорема поотделно, с други думи, каква е последователността от основи и изводи от основите, което задължително води до признаване на истинността на позицията, която се доказва в тази теорема.
Последователността или връзката на основанията и изводите от основанията, водещи до необходимото признаване на истинността на тезата, която се доказва, се нарича метод на доказване или демонстрация. Демонстрацията не е неразделна част от доказателството, а третата, наред с тезата и основанията, които се доказват, логическата характеристика на доказателството.
От тази дефиниция на демонстрация може да се види нейната разлика от съставните части на доказателството, тезата и основата. Както тезата, така и всяка от основите - изявлението на проверен факт, дефиницията, аксиомата, предварително доказаното положение на науката - представлява отделно съждение. Напротив, една демонстрация никога не е индивидуална преценка, нито прост сбор от индивидуални преценки. Демонстрацията винаги е логическа връзка на преценка, водеща до определен логически резултат. Демонстрацията е повече или по-малко дълга верига от изводи, чиито предпоставки са основата на даденото доказателство и чието крайно заключение е тезата, която трябва да се докаже, която по този начин се удостоверява като вярна.
И така, когато доказваме теоремата на евклидовата геометрия за сумата от вътрешните ъгли на триъгълник (виж фиг. 2), първо продължаваме страната на триъгълника ABC, например страната AC до точката E. След това изчертаваме от точката C правата CD, успоредна на AB, и от същата страна на нея от правата AC. Тогава ние се аргументираме по следния начин. Правата BC пресича успоредна (по построение)прави AB и CD. Следователно ъглите ABC и BCD ще бъдат равни като вътрешни кръстосани. Правата AC пресича същите — успоредни по конструкция — прави AB и CD. Следователно ъглите BAC и DCE са равни като съответни. Ъгъл ALL, който е сборът от ъглите BCD и DCE, е равен на сбора от двата вътрешни ъгъла на триъгълника (ABC и BAC), тъй като ъгъл BCD е равен на ъгъл ABC, а ъгъл DCE е равен на ъгъл BAC. Нека добавим ъгъл BCA към ъгъл ALL, третият вътрешен ъгъл на триъгълник ABC. Тогава сборът от ъглите DCE, BCD и BCA ще бъде равен на сбора от вътрешните ъгли на дадения триъгълник: ъглите BAC, ABC и BCA. Но тъй като сборът от ъгли ALL (равен на сбора от ъгли BAC и ABC) и BCA е равен на сбора от два съседни ъгъла и този сбор е равен на два прави ъгъла, тогава сборът от вътрешните ъгли BAC, ABC и BCA в триъгълник ABC също е равен на два прави ъгъла.
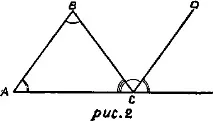
Като цяло, това разсъждение е демонстрация. Основите на доказателството не са отделени в група твърдения, отделени от демонстрацията, но всяка се появява на мястото, което е определено за нея от логическата връзка на всички връзки на демонстрацията.
Тъй като демонстрацията е редът на връзката между основите и тезата - ред, който не се вижда лесно от основите, но такъв, който тепърва ще бъде открит, доказателството на едно и също твърдение на науката може да бъде повече или по-малко сложно или просто, тромаво или кратко и т.н. Самият ред, планът на доказателство може да варира.
Връзката на основанията, водеща до разглеждане на истинността на доказваната теза, не е единствената. И тъй като тази връзка не е дадена заедно със самите основи, а трябва още да бъде открита, изяснена, намерена, доказването е творческата задача на науката, която се решава с творчески средства.
В редица специални случаи проблемът с доказателството се оказва толкова труден, че неговото решение изискваот учени до огромни усилия в продължение на цели десетилетия или дори векове. Досега не е намерено доказателство на теоремата на Ферма, че уравнението x n = y n +z n не може да има решения за всички цели числа на n големи deEux. В продължение на почти две хилядолетия и половина съществуването на атома остава недоказано, докато успехите на най-новата експериментална и теоретична физика най-накрая донесоха това доказателство. Блестящото предположение на Джордано Бруно за съществуването на планети, въртящи се около други звезди, получи убедително потвърждение едва през последните десетилетия. Във всички тези случаи учените трябваше да положат много усилия, за да докажат това, което можеше да бъде доказано само при определени условия за развитие на наблюдение, експеримент и теоретичен анализ.
От друга страна, когато проблемът с доказателството беше успешно решен, начините и средствата за решаването му бяха различни за различните учени. Още древната математика не познаваше нито едно доказателство на Питагоровата теорема, а редица такива доказателства. И това е типично за доказателство. Тезата, която трябва да се докаже, е една, логическите закони на мисленето са едни и същи, но методите, водещи до признаването на истинността на тезата, могат да бъдат различни. Тези методи се определят от: 1) основанията, от които се извежда тезата, 2) връзката между основанията и тезата. Тази връзка не се вижда от основанията, взети отделно. Намира се чрез изследване на връзката между тезата, която се доказва, и това, което вече е доказано.
Но тъй като е възможно да се премине от тезата, която се доказва, към вече доказаните твърдения по повече от един начин, доказателството може да се развива и подобрява. От примитивни методи за доказване, базирани на неточни, приблизителни и следователно често погрешни визуални представяния, до съвременнидоказателства, основани на точно дефинирани понятия, на аксиоми, независими една от друга, свободни от противоречия, достатъчни на брой, както и на изключително стриктно доказани теореми, практиката на доказване е извървяла дълъг път към усъвършенстване и усъвършенстване. Логическата теория на доказателството се промени и усъвършенства съответно.