32 Основни разлики между линейни и нелинейни системи
1.На линия системи, използваме метода на суперпозиция.
В Нелин. Системи, методът на суперпозиция не е приложим.
2.Линия за стабилност. системи зависи само от свойствата на самата система и не зависи от големината на самия сигнал.
При нелинейните системи устойчивостта се определя от параметрите на системата, нач. условия и амплитуда на входния сигнал. Стабилността на нелинейната система се оценява по 3 критерия:
– устойчивост в малкото е устойчивостта на системата при безкрайно малки отклонения от началния режим. При малко по-големи отклонения системата става нестабилна.
- системата е стабилна в големи, ако системата е стабилна за безкрайно големи отклонения, които са възможни в тази система. При малки стойности системата може да е нестабилна.
- системата е стабилна като цяло, ако системата е стабилна при всякакви влияния.
3.В линейните системи, при отсъствие на външно въздействие, никога не възниква стабилно трептене (самотрептение). Това колебание е възможно само в система, която е на границата на стабилността, но това състояние е нестабилно. Малка промяна в параметрите на системата може да доведе до нестабилно или стабилно състояние.
В нелинейните системи са характерни автотрептения, които се причиняват само от свойствата на самата система, т.е. не са отговор на външни влияния. В този случай може да има няколко автоколебателни режима с различни амплитуди и честоти.
33 Устойчивост на НСАУ. Метод на хармоничния баланс.
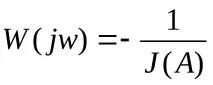
В този случай той ще бъде динамично стабилен. система, т.е. влиза в режим на автоколебане.
Нека начертаем това на графика:
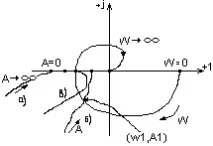
A: 0…
а) ако ходографите не се пресичат =>няма решения на уравнението => няма автоколебания.
б) ако ходографите се пресичат, тогава се дефинират м. пресечки. честота на трептене и специфични. амплитуда, т.е. пар-ри (режим) автоколебания.
c) Ходографите се пресичат два пъти (или няколко).
Методът се използва за изследване на устойчивостта и собствените трептения на линейна система. С помощта на този метод се изследва липсата на трептения в нелинейна затворена система и се изследват собствените трептения.
x = asinwt