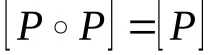3.2. Свойства на бинарните отношения.

Разгледайтеспециалнитесвойства на бинарните отношения в множествотоA.

Свойства на бинарните отношения.

1. Връзка  върхуAAсе наричарефлексивна, ако (a,a) принадлежи на  за всичкиaотA.

2. Отношение  се наричаантирефлексивно, ако (a,b) предполагаab.

3. Отношението е симетрично, ако заaиb, принадлежащи наA, от (a,b) следва, че (b,a).

4. The relation  is calledantisymmetric, if foraandbfromA, from the membership of (a,b) and (b,a) to the relation  it follows thata=b.

Релациите "=" и "£" са рефлексивни релации върху множеството N, но релацията "-1 е равна на транспонираната матрица на релацията P:

.

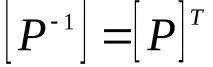
Ако , тогава

.

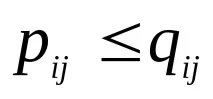
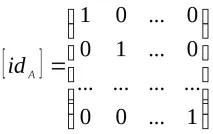
Матрицата на връзката на идентичността idA е единична:

ПРИМЕР 2. Нека

са матрици на отношения P и Q. Тогава

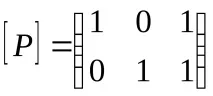
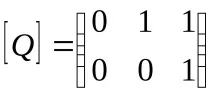
Ако

тогава

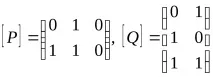
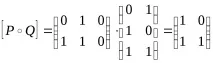
Нека разгледаме свойствата на отношенията на езика на матриците.

Нека P е двоично отношение в множеството

.

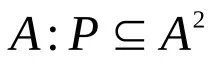
рефлексивно, ако на главния диагонал на релационната матрица са разположени само единици;

симетричен, ако матрицата е симетрична спрямо главния диагонал;

антисиметричен, ако в матрицата

всички елементи извън главния диагонал са нула;

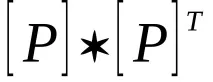
е транзитивно, ако релацията

е изпълнена.

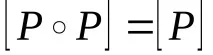
ПРИМЕР 4. Нека проверим какви свойства притежава релацията

, A=, показана на фигурата.

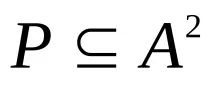
С

напуснете релационната матрица Р:

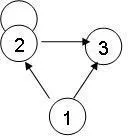
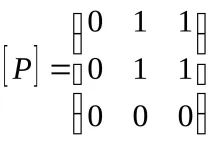
Тъй като матрицата

има нулеви елементи на главния диагонал, отношението Рне е рефлексивно.

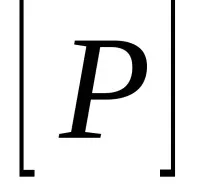
Асиметрия на матрицата

означава, че отношението Pне е симетрично.

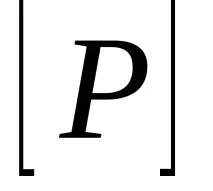
За да проверим антисиметрията, изчисляваме матрицата.

Тъй като в получената матрица всички елементи извън главния диагонал са нула, отношението Ре антисиметрично.

Тъй като

(проверете!), тоест P етранзитивнарелация.

---