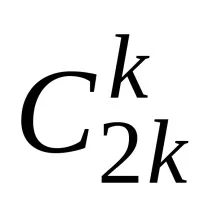3.3. Методи за избор на криви на растеж за подравняване
Трудността при решаването на проблема с избора на най-добрата крива е следната: да предположим, че има времева серия, състояща се отnнива, както и(n-1)полином, който точно описва тази времева серия. Освен това е възможно да се изберат безкраен брой полиноми от по-висок порядък, както и функции от друг тип, които ще апроксимират изследвания времеви ред с достатъчна степен на точност. В този случай няма причина да давате предпочитание на някоя от избраните функции. Следователно, проблемът не е да се намери функция, която следва точно времевия ред, а да се гарантира, че монтираната функция осигурява приемливо съгласие с наличните данни и в същото време дава правдоподобно описание на разглеждания феномен. Последното изискване може да бъде изпълнено, ако апроксимиращата крива се приеме като експоненциална, параболична (от нисък ред), S-образна или друга сравнително проста функция, която позволява да се интерпретира развитието на процеса, който се изследва.
Въз основа на горните предположения ще разгледаме най-често срещаните методи за избор на криви на растеж. Най-простият метод е визуален. По този метод се изгражда графика на времевия ред и се избира такава крива на растеж, чиято форма съответства на реалното развитие на процеса. Ако тенденцията не е ясно видима на оригиналната графика, нивата на серията се подравняват, след което се изгражда нова графика и се избира функцията, съответстваща на графиката на подравнената серия. Въпреки това, възможността за грешка или субективно вземане на решение при използване на визуален метод е висока. Различните изследователи на базата на една и съща графика могат да стигнат до различни заключения при избора на формата на кривата. Прилагането на визуален подход е значително опростено сс помощта на графичен софтуер.
Вторият метод, използван за избор на типа полиномна крива на нарастване, е методът на крайните разлики (метод на Тинтнер). Този метод може да се използва за предварително избиране на полиномна крива, като се правят следните допускания:
1. Нивата на времевите редове се състоят само от два компонента: систематичен компонент (тенденция) и случаен компонент
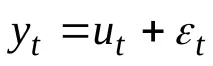
където


2. тенденцията е доста гладка и следователно може да бъде елиминирана или намалена чрез образуване на последователни разлики;
3. Случайният компонент

Изборът на крива на растеж с помощта на метода на крайните разлики е както следва:
1. Разликитеk-ти ред се изчисляват с помощта на рекурсивни отношения
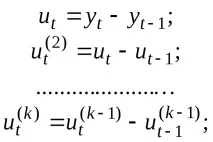
2. Дисперсиите се изчисляват за първоначалната серия и за всяка серия от разлики, като се използват следните формули:
за оригиналната серия по обичайната формула
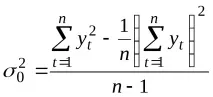
заk-та серия от разлики съгласно формулата
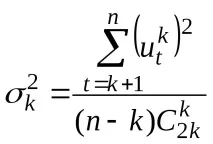
където