4.2.4 Изчисляване на извадкова статистика
Изчисляването на статистически характеристики също се извършва за всяка статистическа съвкупност от пет.
Смята се, че законът за разпределение на случайните грешки е дефиниран в точка 4.2.2. тези. предварително е определено дали законът за разпределение е нормален или не.
Наборът от стойности на случайна променлива, получена в резултат на експеримент или наблюдения върху обекта на изследване, е статичен набор.
Когато експериментите се повтарят при същите условия, обикновено се открива модел в честотата на поява на определени резултати. Някои стойности на случайна променлива се появяват много по-често от други, докато като цяло те са групирани спрямо определена стойност - математическото очакване.
Дисперсията на случайна променлива спрямо математическото очакване се характеризира с величина, наречена дисперсия.
Най-добрата оценка за математическото очакване е средната аритметична извадка:
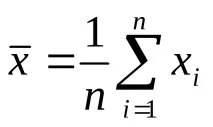
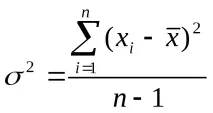
Стойността на σ е оценка на стандартното отклонение на извадката (RMS).
4.2.5 Отсяване на аномални стойности
Може да е трудно да се направи граница между резултат, съдържащ пропуск и резултат, който е надежден, и да се назоват резултати, които съдържат очевидни пропуски. За нормално разпределена проба с размер 6